04. MLR실습

Applied statistics
Author

김보람

Published

April 18, 2023

해당 자료는 전북대학교 이영미 교수님 2023응용통계학 자료임

선형회귀분석 CH0607

library(MASS)
library(lmtest)
Loading required package: zoo


Attaching package: ‘zoo’


The following objects are masked from ‘package:base’:

    as.Date, as.Date.numeric

데이터(Boston)

data(Boston)
head(Boston)
A data.frame: 6 × 14
crim zn indus chas nox rm age dis rad tax ptratio black lstat medv
<dbl> <dbl> <dbl> <int> <dbl> <dbl> <dbl> <dbl> <int> <dbl> <dbl> <dbl> <dbl> <dbl>
1 0.00632 18 2.31 0 0.538 6.575 65.2 4.0900 1 296 15.3 396.90 4.98 24.0
2 0.02731 0 7.07 0 0.469 6.421 78.9 4.9671 2 242 17.8 396.90 9.14 21.6
3 0.02729 0 7.07 0 0.469 7.185 61.1 4.9671 2 242 17.8 392.83 4.03 34.7
4 0.03237 0 2.18 0 0.458 6.998 45.8 6.0622 3 222 18.7 394.63 2.94 33.4
5 0.06905 0 2.18 0 0.458 7.147 54.2 6.0622 3 222 18.7 396.90 5.33 36.2
6 0.02985 0 2.18 0 0.458 6.430 58.7 6.0622 3 222 18.7 394.12 5.21 28.7

  • 보스턴 집값 데이터 이 데이터는 보스턴 근교 지역의 집값 및 다른 정보를 포함한다.

  • MASS 패키지를 설치하면 데이터를 로딩할 수 있다.

  • B보스턴 근교 506개 지역에 대한 범죄율 (crim)등 14개의 변수로 구성

• crim : 범죄율

• zn: 25,000평방비트 기준 거지주 비율

• indus: 비소매업종 점유 구역 비율

• chas: 찰스강 인접 여부 (1=인접, 0=비인접)

• nox: 일산화질소 농도 (천만개 당)

• rm: 거주지의 평균 방 갯수 ***

• age: 1940년 이전에 건축된 주택의 비율

• dis: 보스턴 5대 사업지구와의 거리

• rad: 고속도로 진입용이성 정도

• tax: 재산세율 (10,000달러 당)

• ptratio: 학생 대 교사 비율

• black: 1000(B − 0.63)2, B: 아프리카계 미국인 비율

• lstat : 저소득층 비율 ****

• medv: 주택가격의 중앙값 (단위:1,000달러 당) 반응변수

산점도

pairs(Boston[,which(names(Boston) %in% 
                      c('medv', 'rm', 'lstat'))], 
      pch=16, col='darkorange')

  • 마지막 행을 봐보자. 맨아래 왼쪽의 X축은 rm, Y축은 medv를 의미하고, 맨아래의 중간의 x축은 lstat를 의미한다.

  • rm이 클수록 집값이 증가하고(직선관계처럼 보인다)

  • lstat가 높아질수록 집값은 떨어지는 경향이 있다(곡선관계처럼 보인다. 처음엔 뚝 떨어지다가 천천히 감소)

  • rm과 lstat의 다중공산성을 봐야해! > 맨위 가운데 그림을 봐보자..

상관관계

# pairs(Boston, pch=16, col='darkorange')
cor(Boston[,which(names(Boston) %in% 
                    c('medv', 'rm', 'lstat'))])
A matrix: 3 × 3 of type dbl
rm lstat medv
rm 1.0000000 -0.6138083 0.6953599
lstat -0.6138083 1.0000000 -0.7376627
medv 0.6953599 -0.7376627 1.0000000

  • rm과 medv는 양의 상관관계

  • lstat와 mdev는 음의 상관관계

  • rm과 lstat는 음의 상관관계

회귀모형 적합

fit_Boston<-lm(medv~rm+lstat, data=Boston)
summary(fit_Boston)

Call:
lm(formula = medv ~ rm + lstat, data = Boston)

Residuals:
    Min      1Q  Median      3Q     Max 
-18.076  -3.516  -1.010   1.909  28.131 

Coefficients:
            Estimate Std. Error t value Pr(>|t|)    
(Intercept) -1.35827    3.17283  -0.428    0.669    
rm           5.09479    0.44447  11.463   <2e-16 ***
lstat       -0.64236    0.04373 -14.689   <2e-16 ***
---
Signif. codes:  0 ‘***’ 0.001 ‘**’ 0.01 ‘*’ 0.05 ‘.’ 0.1 ‘ ’ 1

Residual standard error: 5.54 on 503 degrees of freedom
Multiple R-squared:  0.6386,    Adjusted R-squared:  0.6371 
F-statistic: 444.3 on 2 and 503 DF,  p-value: < 2.2e-16

  • \(y=\beta_0 + \beta_1 x_1 + \beta_2 x_2 + \epsilon , \ \epsilon\) ~ \(N(0,\sigma^2)\)

  • 모형을 적합하라는 것은, \(\hat \beta_0, \hat \beta_1, \hat \beta_2\)를 구해서 \(\hat y=\)꼴로 적어주기

- summary 결과 해석

  • 회귀직선의 유의성에 대한 가설검정이다.

  • \(H_0: \beta_1=\beta_2=0\) vs \(H_1: \beta_1 \neq 0\) or \(\beta_2 \neq 0\)

  • F-statistic: 444.3, F=MSR/MSE, p-value: < 2.2e-16:p-value가 아주 작으므로 \(H_0\)를 기각할 수 있다. 즉 회귀직선은 유의하다.

  • Residual standard error: 5.54 = \(\sqrt{MSE} = \sqrt{\widehat \sigma^2} = \widehat \sigma^2\)

  • Pr(>|t|):양측 검정에 대한 유의성 검정

  • Estimate 추정량, \(\hat \beta_0=-1.35827, \hat \beta_1=5.09479, \hat \beta_2=-0.64236\)

  • Std. Error = \(s.e(\widehat \beta_i) = \dfrac{\sigma^2}{c_{ii}}\) 이고, \(\widehat {s.e}(\widehat \beta_i)\sqrt{\dfrac{\widehat \sigma^2}{c_{ii}}}\)

  • t value는 \(t_0 = \dfrac{\widehat \beta_i - 0}{\widehat {s.e}(\widehat \beta_i)}\)

  • 절편은 유의하지 않다.

  • Residuals: 잔차해석. 0을 기준으로 대칭인가? 봤는데 max가 훨씬 더 커서 오른쪽으로 꼬리가 더 길 수 있겠네? 생각 가능

matrix


n = nrow(Boston)
X = cbind(rep(1,n), Boston$rm, Boston$lstat)
y = Boston$medv
head(X) # 506X3 행렬
A matrix: 6 × 3 of type dbl
1 6.575 4.98
1 6.421 9.14
1 7.185 4.03
1 6.998 2.94
1 7.147 5.33
1 6.430 5.21 
head(y) # medv값, 506x1행렬
  1. 24
  2. 21.6
  3. 34.7
  4. 33.4
  5. 36.2
  6. 28.7
# beta = 3x1 행렬

y = X\(\beta\) + \(\epsilon \rightarrow \widehat \beta = (X^TX)^{-1}X^Ty\)

beta_hat = solve(t(X)%*%X) %*% t(X) %*% y   # t(X): X^T를 의미함 
beta_hat
coef(fit_Boston)
A matrix: 3 × 1 of type dbl
-1.3582728
5.0947880
-0.6423583
(Intercept)
-1.35827281187452
rm
5.09478798433654
lstat
-0.642358334244129

  • t(X): \(X^T\)를 의미

  • %*% : 행렬곱의미

  • solve() : 역행렬 구하는 함수

  • \(\widehat y = X \widehat \beta\)

y_hat = X %*% beta_hat
y_hat[1:5]
fitted(fit_Boston)[1:5]
  1. 28.9410136806025
  2. 25.4842056605591
  3. 32.6590747685798
  4. 32.4065199998349
  5. 31.6304069906576
1
28.941013680603
2
25.4842056605591
3
32.6590747685798
4
32.4065199998349
5
31.6304069906576
  • y_hat[1:5] 과 fitted(fit_Boston)[1:5] 값이 동일한 것을 확인 가능
sse <- sum((y - y_hat)^2) ##SSE
sqrt(sse/(n-2-1)) ##RMSE
summary(fit_Boston)$sigma
5.54025736698867
5.54025736698867

  • \(SSE = \sum (y_i - \widehat y_i)^2\)

  • \(RMSE = \sqrt{SSE/(n-p-1)} = \widehat \sigma\)

lm사용

dt <- Boston[,which(names(Boston) %in% c('medv', 'rm', 'lstat'))]
head(dt)
A data.frame: 6 × 3
rm lstat medv
<dbl> <dbl> <dbl>
1 6.575 4.98 24.0
2 6.421 9.14 21.6
3 7.185 4.03 34.7
4 6.998 2.94 33.4
5 7.147 5.33 36.2
6 6.430 5.21 28.7 
fit_Boston<-lm(medv~., data=dt)           # boston의 설명변수 13개 모두 다 사용하고 싶을때 (물결 뒤에 점을 찍어주기!!)
fit_Boston<-lm(medv~rm+lstat, data=dt)    # 설명변수 중 원하는 것만 사용하고 싶을때
summary(fit_Boston)

Call:
lm(formula = medv ~ rm + lstat, data = dt)

Residuals:
    Min      1Q  Median      3Q     Max 
-18.076  -3.516  -1.010   1.909  28.131 

Coefficients:
            Estimate Std. Error t value Pr(>|t|)    
(Intercept) -1.35827    3.17283  -0.428    0.669    
rm           5.09479    0.44447  11.463   <2e-16 ***
lstat       -0.64236    0.04373 -14.689   <2e-16 ***
---
Signif. codes:  0 ‘***’ 0.001 ‘**’ 0.01 ‘*’ 0.05 ‘.’ 0.1 ‘ ’ 1

Residual standard error: 5.54 on 503 degrees of freedom
Multiple R-squared:  0.6386,    Adjusted R-squared:  0.6371 
F-statistic: 444.3 on 2 and 503 DF,  p-value: < 2.2e-16
  • hat y = -1.3583 + 5.0948rm - 0.6424lstat

분산분석:회귀직선의 유의성 검정

  • \(H_0: \beta_1=\beta_2=0\) vs \(H_1: \beta_1 \neq 0\) or \(\beta_2 \neq 0\)

  • \(H_0\): 귀무가설, null hypothesis, 영가설 -> \(y=\beta_0\)

  • \(H_1\): 대립가설 -> \(y= \beta_0 + \beta_1 x_1 + \beta_2 x_2\)

anova(fit_Boston) ## XXX
A anova: 3 × 5
Df Sum Sq Mean Sq F value Pr(>F)
<int> <dbl> <dbl> <dbl> <dbl>
rm 1 20654.42 20654.41622 672.9039 8.266887e-95
lstat 1 6622.57 6622.56999 215.7579 6.669365e-41
Residuals 503 15439.31 30.69445 NA NA
  • 설명변수가 두개로 쪼개져서 나온다.
null_model <- lm(medv~1, data=dt)  #H0
fit_Boston <- lm(medv~., data=dt)  #H1

anova(null_model, fit_Boston) ##***
A anova: 2 × 6
Res.Df RSS Df Sum of Sq F Pr(>F)
<dbl> <dbl> <dbl> <dbl> <dbl> <dbl>
1 505 42716.30 NA NA NA NA
2 503 15439.31 2 27276.99 444.3309 7.008455e-112

  • null_model : 설명모델을 안쓰고 절편만 가져가는 모델. 1만 쓴다.(절편만)

  • RSS의 \(15439.31=SSE=\sum(y_i - \widehat y_i)^2\)이고 \(42716.30 = \sum(y_i - \bar y)^2=SST\)

  • SST와 SSE를 비교해서 적합이 잘 되어있는지 확인

  • Sum of Sq의 \(27276.99=SSR\)

  • F = \(\dfrac{SSR/P}{SSE/(n-p-1)}\)

\(\beta\)의 신뢰구간

\(\widehat \beta_i \pm t_{a/2} (n-p-1) \widehat{s.e}(\widehat \beta_i)\)

vcov(fit_Boston)  ##var(hat beta) = (X^TX)^-1 \sigma^2
A matrix: 3 × 3 of type dbl
(Intercept) rm lstat
(Intercept) 10.06683612 -1.39248641 -0.099178133
rm -1.39248641 0.19754958 0.011930670
lstat -0.09917813 0.01193067 0.001912441

  • 공분산 행렬 값

  • \(Var(\widehat \beta_1)=0.19754958, Var(\widehat \beta_2)= 0.001912441\)

#코드
confint(fit_Boston, level = 0.90)

#수식(직접계산)
coef(fit_Boston) + qt(0.975, 503) * summary(fit_Boston)$coef[,2]
coef(fit_Boston) - qt(0.975, 503) * summary(fit_Boston)$coef[,2]
A matrix: 3 × 2 of type dbl
5 % 95 %
(Intercept) -6.5867396 3.8701939
rm 4.3623583 5.8272176
lstat -0.7144229 -0.5702938
(Intercept)
4.87535465808391
rm
5.9680255329079
lstat
-0.556439501179164
(Intercept)
-7.59190028183295
rm
4.22155043576519
lstat
-0.728277167309094

  • \(n=506, p=2\)

  • summary(fit_Boston)$coef[,2] : s.e

평균반응, 개별 y 추정

  • E(Y|x0), y = E(Y|x0) + epsilon
new_dt <- data.frame(rm=7, lstat=10)
predict(fit_Boston, newdata = new_dt)
c(1,7,10)%*%beta_hat  # hat y0 = -1.3583 + 5.0948*7 - 0.6424*10
1: 27.88165973604
A matrix: 1 × 1 of type dbl
27.88166
  • \(x_{0}=\begin{pmatrix} 1 \\ 7 \\ 10 \end{pmatrix}, \widehat{y}_{0}=x_{0}^{T}\beta\)
predict(fit_Boston, 
        newdata = new_dt,
        interval = c("confidence"), 
        level = 0.95)  ##평균반응
A matrix: 1 × 3 of type dbl
fit lwr upr
1 27.88166 27.17347 28.58985 
predict(fit_Boston, newdata = new_dt, 
        interval = c("prediction"), 
        level = 0.95)  ## 개별 y
A matrix: 1 × 3 of type dbl
fit lwr upr
1 27.88166 16.97375 38.78957

절편을 포함하지 않는 회귀직선 (원점을 지나는 회귀직선)

  • \(y=\beta_1 x_1 + \beta_2 x_2\)
fit_Boston0 <- lm(medv ~ 0 + rm + lstat, dt)
summary(fit_Boston0)
summary(fit_Boston)

Call:
lm(formula = medv ~ 0 + rm + lstat, data = dt)

Residuals:
    Min      1Q  Median      3Q     Max 
-17.714  -3.498  -1.075   1.877  27.750 

Coefficients:
      Estimate Std. Error t value Pr(>|t|)    
rm     4.90691    0.07019   69.91   <2e-16 ***
lstat -0.65574    0.03056  -21.46   <2e-16 ***
---
Signif. codes:  0 ‘***’ 0.001 ‘**’ 0.01 ‘*’ 0.05 ‘.’ 0.1 ‘ ’ 1

Residual standard error: 5.536 on 504 degrees of freedom
Multiple R-squared:  0.9485,    Adjusted R-squared:  0.9482 
F-statistic:  4637 on 2 and 504 DF,  p-value: < 2.2e-16

Call:
lm(formula = medv ~ ., data = dt)

Residuals:
    Min      1Q  Median      3Q     Max 
-18.076  -3.516  -1.010   1.909  28.131 

Coefficients:
            Estimate Std. Error t value Pr(>|t|)    
(Intercept) -1.35827    3.17283  -0.428    0.669    
rm           5.09479    0.44447  11.463   <2e-16 ***
lstat       -0.64236    0.04373 -14.689   <2e-16 ***
---
Signif. codes:  0 ‘***’ 0.001 ‘**’ 0.01 ‘*’ 0.05 ‘.’ 0.1 ‘ ’ 1

Residual standard error: 5.54 on 503 degrees of freedom
Multiple R-squared:  0.6386,    Adjusted R-squared:  0.6371 
F-statistic: 444.3 on 2 and 503 DF,  p-value: < 2.2e-16

  • \(Adjusted R-squared: 0.9482\) vs \(0.6371\)

  • \(R^2=\dfrac{SSR}{SST}=\dfrac{\sum(\widehat y_i - \bar y)^2}{\sum(y_i-\bar y)^2}\)=\(\dfrac{설명변수 없을때와 있을때의 차이}{y의변동이 평균으로부터 얼마나 떨어져 있는지}\)

  • 절편이 없는 모형의 \(R^2=\dfrac{\sum(\widehat y_i - 0)^2}{\sum(y_i-0)^2}\): 원점으로부터 얼마나 떨어져있는가. 기본적으로 엄청 큰 값을 가지게 된다.

절편이 있다 vs 절편이 없다 에서는 \(R^2\)과 \(RMSE=\widehat \sigma\)를 확인해주는 게 좋다.

RMSE비교 \(5.536\) vs \(5.54\) -> 별로 차이가 없네?

잔차분석

  • epsilon : 선형성, 등분산성, 정규성, 독립성
yhat <- fitted(fit_Boston)
res <- resid(fit_Boston)
plot(res ~ yhat,pch=16, ylab = 'Residual')
abline(h=0, lty=2, col='grey')

  • 선형성 애매함

등분산성

  • H0 : 등분산 vs. H1 : 이분산 (Heteroscedasticity)
bptest(fit_Boston)

    studentized Breusch-Pagan test

data:  fit_Boston
BP = 1.5297, df = 2, p-value = 0.4654
  • p-value가 커서 기각을 못했다. 즉 등분산이다.

정규성

  • 잔차의 QQ plot
par(mfrow=c(1,2))
qqnorm(res, pch=16)
qqline(res, col = 2)

hist(res)
par(mfrow=c(1,1))

  • 이상치가 있는 듯 하다ㅡ

  • Shapiro-Wilk Test


## H0 : normal distribution  vs. H1 : not H0
shapiro.test(res)

    Shapiro-Wilk normality test

data:  res
W = 0.9098, p-value < 2.2e-16
  • 정규분포 아니다

독립성 검정 DW test

  • H0 : uncorrelated vs H1 : rho != 0
dwtest(fit_Boston, alternative = "two.sided") 

    Durbin-Watson test

data:  fit_Boston
DW = 0.83421, p-value < 2.2e-16
alternative hypothesis: true autocorrelation is not 0
  • 독립이라고 할 수 없다.

가설검정: FM, RM

reduced_model = lm(medv ~ rm+lstat, data = Boston) #(q=2) 
full_model = lm(medv ~ ., data=Boston) #(P=13) full model

# r=p-q=11
summary(full_model)
summary(reduced_model)

Call:
lm(formula = medv ~ ., data = Boston)

Residuals:
    Min      1Q  Median      3Q     Max 
-15.595  -2.730  -0.518   1.777  26.199 

Coefficients:
              Estimate Std. Error t value Pr(>|t|)    
(Intercept)  3.646e+01  5.103e+00   7.144 3.28e-12 ***
crim        -1.080e-01  3.286e-02  -3.287 0.001087 ** 
zn           4.642e-02  1.373e-02   3.382 0.000778 ***
indus        2.056e-02  6.150e-02   0.334 0.738288    
chas         2.687e+00  8.616e-01   3.118 0.001925 ** 
nox         -1.777e+01  3.820e+00  -4.651 4.25e-06 ***
rm           3.810e+00  4.179e-01   9.116  < 2e-16 ***
age          6.922e-04  1.321e-02   0.052 0.958229    
dis         -1.476e+00  1.995e-01  -7.398 6.01e-13 ***
rad          3.060e-01  6.635e-02   4.613 5.07e-06 ***
tax         -1.233e-02  3.760e-03  -3.280 0.001112 ** 
ptratio     -9.527e-01  1.308e-01  -7.283 1.31e-12 ***
black        9.312e-03  2.686e-03   3.467 0.000573 ***
lstat       -5.248e-01  5.072e-02 -10.347  < 2e-16 ***
---
Signif. codes:  0 ‘***’ 0.001 ‘**’ 0.01 ‘*’ 0.05 ‘.’ 0.1 ‘ ’ 1

Residual standard error: 4.745 on 492 degrees of freedom
Multiple R-squared:  0.7406,    Adjusted R-squared:  0.7338 
F-statistic: 108.1 on 13 and 492 DF,  p-value: < 2.2e-16

Call:
lm(formula = medv ~ rm + lstat, data = Boston)

Residuals:
    Min      1Q  Median      3Q     Max 
-18.076  -3.516  -1.010   1.909  28.131 

Coefficients:
            Estimate Std. Error t value Pr(>|t|)    
(Intercept) -1.35827    3.17283  -0.428    0.669    
rm           5.09479    0.44447  11.463   <2e-16 ***
lstat       -0.64236    0.04373 -14.689   <2e-16 ***
---
Signif. codes:  0 ‘***’ 0.001 ‘**’ 0.01 ‘*’ 0.05 ‘.’ 0.1 ‘ ’ 1

Residual standard error: 5.54 on 503 degrees of freedom
Multiple R-squared:  0.6386,    Adjusted R-squared:  0.6371 
F-statistic: 444.3 on 2 and 503 DF,  p-value: < 2.2e-16

  • reduced_model보다는 full_model이 더 좋아 보인다. (R^2와 RMSE확인햇을떄)

  • 13개 중 11개 변수가 유의함을 확인 가능

가설검정

RM : \(H_0: \beta_1= \dots = \beta_5 = \beta_7 = \dots = \beta_{12} = 0\)

anova(reduced_model, full_model)
A anova: 2 × 6
Res.Df RSS Df Sum of Sq F Pr(>F)
<dbl> <dbl> <dbl> <dbl> <dbl> <dbl>
1 503 15439.31 NA NA NA NA
2 492 11078.78 11 4360.525 17.60431 1.425983e-29

\(F = \dfrac{(SSE_{RM}-SSE_{RM})/r}{SSE_{FM}/(n-p-1)}=\dfrac{(SSR_{FM}-SSR_{RM})/r}{SSE_{FM}/(n-p-1)}=17.60431\)

  • RSS : SSE를 의미. RM의 \(SSE=15439.31\), FM의 \(SSE=11078.78\)

  • Res.Df: \(n-q-1=503, n-p-1=492\)

#강의록에 있는 수식
p <- full_model$rank-1
q <- reduced_model$rank-1
SSE_FM <- anova(full_model)$Sum[p+1] #SSE_FM
SSE_RM <- anova(reduced_model)$Sum[q+1]  #SSE_RM

F0 <- ((SSE_RM-SSE_FM)/(p-q))/(SSE_FM/(nrow(Boston)-p-1))
F0
17.60431143783 
#기각역 F_{0.05}(p-q,n-p-1)
qf(0.95,p-q,nrow(Boston)-p-1)
# p-value -> 해당강의 20분쯤.. 어렵
1-pf(F0, p-q,nrow(Boston)-p-1)
1.80811652913556
0 
#################################
reduced_model = lm(medv ~ .-age-indus, data = Boston)  # 유의하지 않은 2개 변수 제거(-age-indus)
full_model = lm(medv ~ ., data=Boston) # 13개 변수

anova(reduced_model, full_model)
A anova: 2 × 6
Res.Df RSS Df Sum of Sq F Pr(>F)
<dbl> <dbl> <dbl> <dbl> <dbl> <dbl>
1 494 11081.36 NA NA NA NA
2 492 11078.78 2 2.579374 0.05727398 0.9443416
  • \(H_0: \beta_{indus} = \beta_{age} = 0\) 이고 H0기각 못하므로 빼도 된다.

General linear hypothesis

  • 선형 가설 검정
x1<-c(4,8,9,8,8,12,6,10,6,9)
x2<-c(4,10,8,5,10,15,8,13,5,12)
y<-c(9,20,22,15,17,30,18,25,10,20)
fit<-lm(y~x1+x2)  ##FM
summary(fit)

Call:
lm(formula = y ~ x1 + x2)

Residuals:
    Min      1Q  Median      3Q     Max 
-2.4575 -1.9100  0.3314  0.6388  3.2628 

Coefficients:
            Estimate Std. Error t value Pr(>|t|)  
(Intercept)  -0.6507     2.9075  -0.224   0.8293  
x1            1.5515     0.6462   2.401   0.0474 *
x2            0.7599     0.3968   1.915   0.0970 .
---
Signif. codes:  0 ‘***’ 0.001 ‘**’ 0.01 ‘*’ 0.05 ‘.’ 0.1 ‘ ’ 1

Residual standard error: 2.278 on 7 degrees of freedom
Multiple R-squared:  0.9014,    Adjusted R-squared:  0.8732 
F-statistic:    32 on 2 and 7 DF,  p-value: 0.0003011
  • \(H_0 : T\beta = c\)
# install.packages("car")
  • \(H_0 : \beta_1 = 1\)

\(y=\beta_0 + \beta_1 x_1 + \beta_2 x_2 + \epsilon\) 에서

\(y=\beta_0 + x_1 + \beta_2 x_2 + \epsilon\) 이 된다.

즉, \(y-x_1 = \beta_0 + \beta_2 x_2 + \epsilon\)

단순성형회귀모형이 되는것..(z)

library(car)
linearHypothesis(fit, c(0,1,0), 1)
ERROR: Error in library(car): there is no package called ‘car’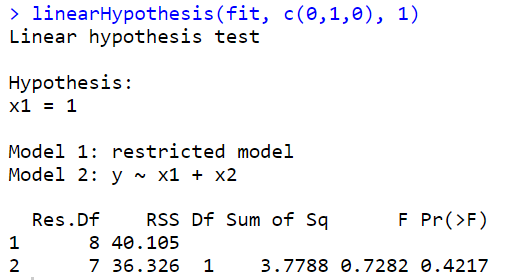
  • 오류가 나넹.. Rstudio에서 돌린거

  • 기각 못한다. beta1=1

  • \(H_0 : \beta_1 = \beta_2\)

#b1-b2=0 => (0,1,-1) *beta 
#H_0 : beta_1 = beta2
linearHypothesis(fit, c(0,1,-1), 0)

  • \(H_0 : \beta_1 = \beta_2+1\)
#H_0 : beta_1 = beta2 + 1
linearHypothesis(fit, c(0,1,-1), 1)

  • \(H_0 : \beta_1 = \beta_2+5\)
#H_0 : beta_1 = beta2 + 5
linearHypothesis(fit, c(0,1,-1), 5)

  • 5로 바꾸고 나니까 기각할 수 있다.

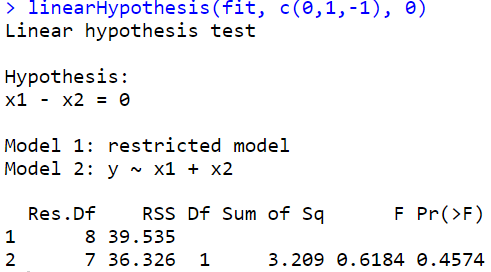
- 강의노트 코드

##H_0 : beta_1 = beta2 + 1
#y=b0 + b1x1 + b2x2 + e = b0+x1 + b2(x1+x2)+e
#y-x1 = b0+b2(x1+x2)+e :   RM
y1 <- y-x1
z1 <- x1 + x2
fit2 <- lm(y1~z1)
summary(fit2)
anova(fit2)

Call:
lm(formula = y1 ~ z1)

Residuals:
    Min      1Q  Median      3Q     Max 
-2.5054 -1.9294  0.4236  0.6821  3.4473 

Coefficients:
            Estimate Std. Error t value Pr(>|t|)    
(Intercept)  -1.0014     2.2175  -0.452 0.663574    
z1            0.6824     0.1242   5.493 0.000578 ***
---
Signif. codes:  0 ‘***’ 0.001 ‘**’ 0.01 ‘*’ 0.05 ‘.’ 0.1 ‘ ’ 1

Residual standard error: 2.137 on 8 degrees of freedom
Multiple R-squared:  0.7904,    Adjusted R-squared:  0.7642 
F-statistic: 30.17 on 1 and 8 DF,  p-value: 0.0005785
A anova: 2 × 5
Df Sum Sq Mean Sq F value Pr(>F)
<int> <dbl> <dbl> <dbl> <dbl>
z1 1 137.85135 137.851351 30.17378 0.0005784583
Residuals 8 36.54865 4.568581 NA NA 
anova(fit)  ##FM
anova(fit2)  #RM
A anova: 3 × 5
Df Sum Sq Mean Sq F value Pr(>F)
<int> <dbl> <dbl> <dbl> <dbl>
x1 1 313.04348 313.043478 60.323103 0.0001100467
x2 1 19.03040 19.030400 3.667135 0.0970444465
Residuals 7 36.32612 5.189446 NA NA
A anova: 2 × 5
Df Sum Sq Mean Sq F value Pr(>F)
<int> <dbl> <dbl> <dbl> <dbl>
z1 1 137.85135 137.851351 30.17378 0.0005784583
Residuals 8 36.54865 4.568581 NA NA 
# F = {(SSE_RM - SSE_FM)/r} / {SSE_FM/(n-p-1)}
p <- fit$rank-1
q <- fit2$rank-1
SSE_FM <- anova(fit)$Sum[p+1] #SSE_FM
SSE_RM <- anova(fit2)$Sum[q+1]  #SSE_RM
F0 <- ((SSE_RM-SSE_FM)/(p-q))/(SSE_FM/(length(y)-p-1))
F0
0.0428807391894599 
#기각역 F_{0.05}(p-q,n-p-1)
qf(0.95,p-q,length(y)-p-1)
# p-value
pf(F0, p-q,length(y)-p-1,lower.tail = F)
5.59144785122073
0.841844969417543