09. 변수변환 실습

Applied statistics
Author

김보람

Published

May 25, 2023

해당 자료는 전북대학교 이영미 교수님 2023응용통계학 자료임

변수변환

설명변수 변환

wind <- read.csv("wind.csv")
head(wind)
A data.frame: 6 × 3
i x y
<int> <dbl> <dbl>
1 1 5.0 1.582
2 2 6.0 1.822
3 3 3.4 1.057
4 4 2.7 0.500
5 5 10.0 2.236
6 6 9.7 2.386 
par(mfrow=c(1,2))
plot(y~x, wind, pch=16, main="scatter plot") 
abline(wind_fit, col='darkorange', lwd=2)

plot(fitted(wind_fit), rstandard(wind_fit),  pch = 16,
     xlab = expression(hat(y)), 
     ylab = "Standardized Residuals",  
     main = "Fitted vs. Residuals")
abline(h = 0, col = "grey", lwd = 2, lty=2)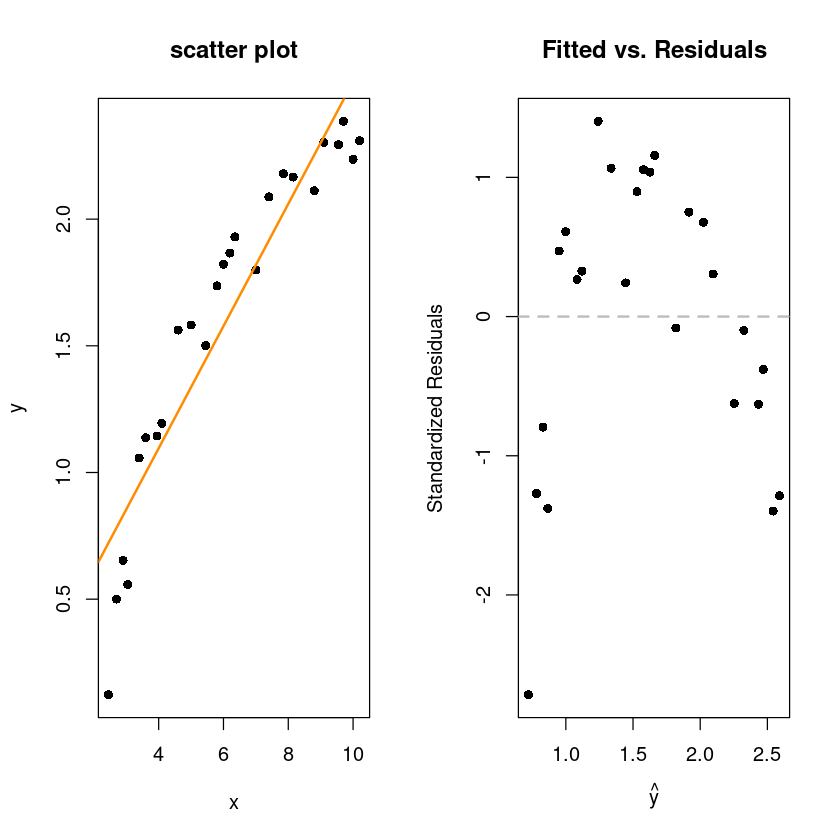

  • 산점도를 봤을때 직선보다는 곡선이 어울려 보이는 산점도

  • 표준화된잔차를 봐도 선형성(2차)이 보인다.

lm1

\(y=\beta_0+\beta_1x+\epsilon\)

wind_fit <- lm(y~x, wind) 
summary(wind_fit)

Call:
lm(formula = y ~ x, data = wind)

Residuals:
     Min       1Q   Median       3Q      Max 
-0.59869 -0.14099  0.06059  0.17262  0.32184 

Coefficients:
            Estimate Std. Error t value Pr(>|t|)    
(Intercept)  0.13088    0.12599   1.039     0.31    
x            0.24115    0.01905  12.659 7.55e-12 ***
---
Signif. codes:  0 ‘***’ 0.001 ‘**’ 0.01 ‘*’ 0.05 ‘.’ 0.1 ‘ ’ 1

Residual standard error: 0.2361 on 23 degrees of freedom
Multiple R-squared:  0.8745,    Adjusted R-squared:  0.869 
F-statistic: 160.3 on 1 and 23 DF,  p-value: 7.546e-12
print(paste0("coefficient of determination : ", round(summary(wind_fit)$r.squared,3)))
[1] "coefficient of determination : 0.874"
  • 단순선형회귀
print(paste0("RMSE : ", round(summary(wind_fit)$sigma,3)))
[1] "RMSE : 0.236"

lm2

\(y=\beta_0+\beta_1x+\beta_2x^2+\epsilon\)

wind_fit_2 <- lm(y~x+I(x^2), wind) 
summary(wind_fit_2)

Call:
lm(formula = y ~ x + I(x^2), data = wind)

Residuals:
     Min       1Q   Median       3Q      Max 
-0.26347 -0.02537  0.01264  0.03908  0.19903 

Coefficients:
             Estimate Std. Error t value Pr(>|t|)    
(Intercept) -1.155898   0.174650  -6.618 1.18e-06 ***
x            0.722936   0.061425  11.769 5.77e-11 ***
I(x^2)      -0.038121   0.004797  -7.947 6.59e-08 ***
---
Signif. codes:  0 ‘***’ 0.001 ‘**’ 0.01 ‘*’ 0.05 ‘.’ 0.1 ‘ ’ 1

Residual standard error: 0.1227 on 22 degrees of freedom
Multiple R-squared:  0.9676,    Adjusted R-squared:  0.9646 
F-statistic: 328.3 on 2 and 22 DF,  p-value: < 2.2e-16

  • \(x^2\)을 넣었더니 모형도 유의하고 \(R^2\)의 값도 커짐

  • 두개 변수 모두 유의함

par(mfrow=c(1,2))
plot(y~x, wind, pch=16, main="scatter plot")
x_new <- sort(wind$x)
lines(x_new, predict(wind_fit_2, newdata = data.frame(x=x_new)), col='darkorange', lwd=2)

plot(fitted(wind_fit_2), rstandard(wind_fit_2),  pch = 16,
      xlab = expression(hat(y)), 
      ylab = "Standardized Residuals",  
      main = "Fitted vs. Residuals")
abline(h = 0, col = "grey", lwd = 2, lty=2)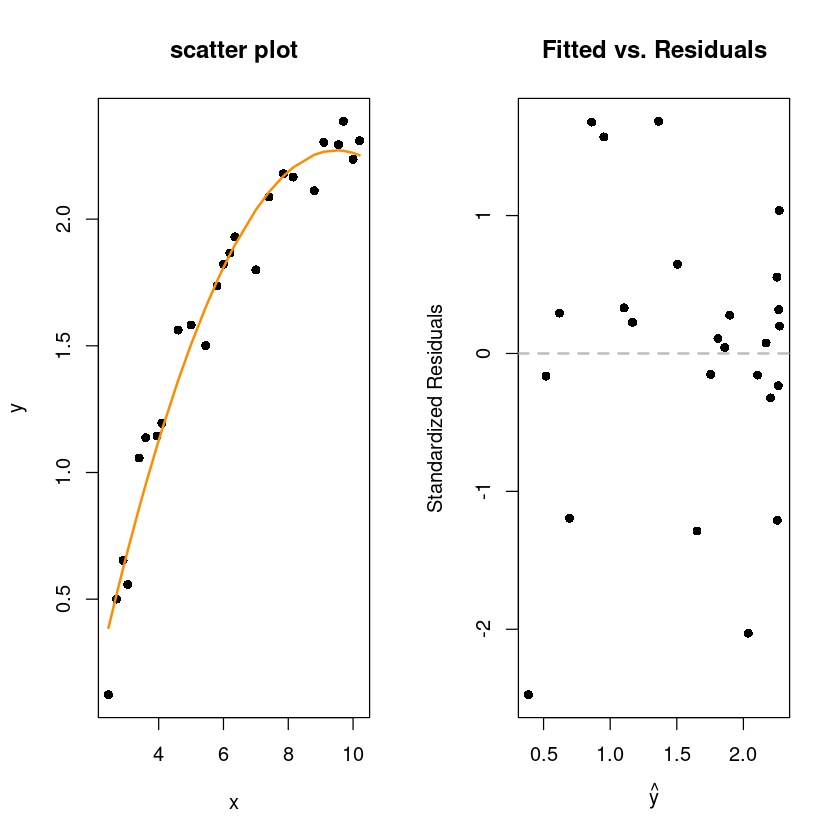

  • fitted line이 데이터를 잘 훑는 거 같이 보인다.
print(paste0("coefficient of determination : ", round(summary(wind_fit_2)$r.squared,3)))
[1] "coefficient of determination : 0.968"
print(paste0("RMSE : ", round(summary(wind_fit_2)$sigma,3)))
[1] "RMSE : 0.123"

lm3

\(y=\beta_0+\beta_1 \dfrac{1}{x}+\epsilon=\beta_0+\beta_1 x^`+\epsilon\)

wind_fit_3 <- lm(y~I(1/x), wind) 
summary(wind_fit_3)

Call:
lm(formula = y ~ I(1/x), data = wind)

Residuals:
     Min       1Q   Median       3Q      Max 
-0.20547 -0.04940  0.01100  0.08352  0.12204 

Coefficients:
            Estimate Std. Error t value Pr(>|t|)    
(Intercept)   2.9789     0.0449   66.34   <2e-16 ***
I(1/x)       -6.9345     0.2064  -33.59   <2e-16 ***
---
Signif. codes:  0 ‘***’ 0.001 ‘**’ 0.01 ‘*’ 0.05 ‘.’ 0.1 ‘ ’ 1

Residual standard error: 0.09417 on 23 degrees of freedom
Multiple R-squared:   0.98, Adjusted R-squared:  0.9792 
F-statistic:  1128 on 1 and 23 DF,  p-value: < 2.2e-16
par(mfrow=c(1,2))
plot(y~I(1/x), wind, pch=16, main="scatter plot") 
abline(wind_fit_3, col='darkorange', lwd=2)

plot(fitted(wind_fit_3), rstandard(wind_fit_3),  pch = 16,
     xlab = expression(hat(y)), 
     ylab = "Standardized Residuals",  
     main = "Fitted vs. Residuals")
abline(h = 0, col = "grey", lwd = 2, lty=2)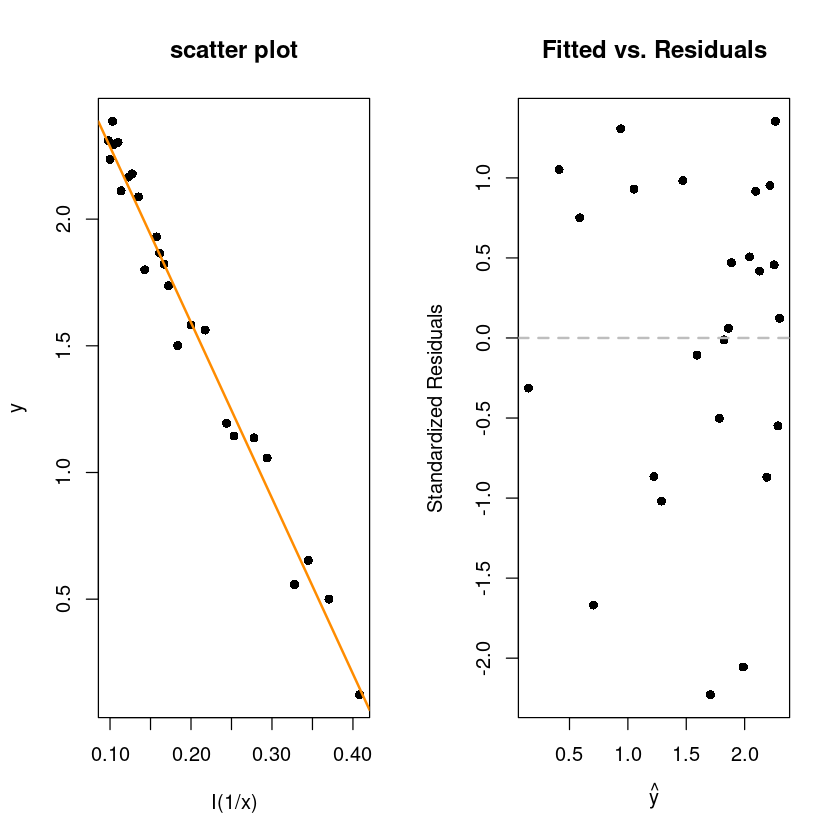

print(paste0("coefficient of determination : ", round(summary(wind_fit_3)$r.squared,3)))
[1] "coefficient of determination : 0.98"
print(paste0("RMSE : ", round(summary(wind_fit_3)$sigma,3)))
[1] "RMSE : 0.094"

반응변수 변환

initech <- read.csv("initech.csv")
head(initech)
A data.frame: 6 × 2
years salary
<int> <int>
1 1 41504
2 1 32619
3 1 44322
4 2 40038
5 2 46147
6 2 38447 
par(mfrow=c(1,1))
plot(salary~years, initech,  pch=16, cex=1.5)

  • 곡선 관계!?

  • x가 증가하면서 y값이 점점 퍼지고 있다. x가 증가할수록 salary의 분산이 커지고 있다.

LM1

\(y=\beta_0+\beta_x+\epsilon\)

initech_fit <- lm(salary~years, initech) 
summary(initech_fit)

Call:
lm(formula = salary ~ years, data = initech)

Residuals:
   Min     1Q Median     3Q    Max 
-57225 -18104    241  15589  91332 

Coefficients:
            Estimate Std. Error t value Pr(>|t|)    
(Intercept)     5302       5750   0.922    0.359    
years           8637        389  22.200   <2e-16 ***
---
Signif. codes:  0 ‘***’ 0.001 ‘**’ 0.01 ‘*’ 0.05 ‘.’ 0.1 ‘ ’ 1

Residual standard error: 27360 on 98 degrees of freedom
Multiple R-squared:  0.8341,    Adjusted R-squared:  0.8324 
F-statistic: 492.8 on 1 and 98 DF,  p-value: < 2.2e-16
plot(salary~years, initech,
        pch=16, cex=1.5)
abline(initech_fit, col='darkorange', lwd=2)

par(mfrow=c(1,2))

plot(fitted(initech_fit), rstandard(initech_fit),  pch = 16,
     xlab = expression(hat(y)), 
     ylab = "Standardized Residuals",  
     main = "Fitted versus Residuals")
abline(h = 0, col = "grey", lwd = 2, lty=2)

qqnorm(resid(initech_fit), pch=16,
          main = "Normal Q-Q Plot", col = "darkgrey") 
qqline(resid(initech_fit), col = "dodgerblue", lwd = 2)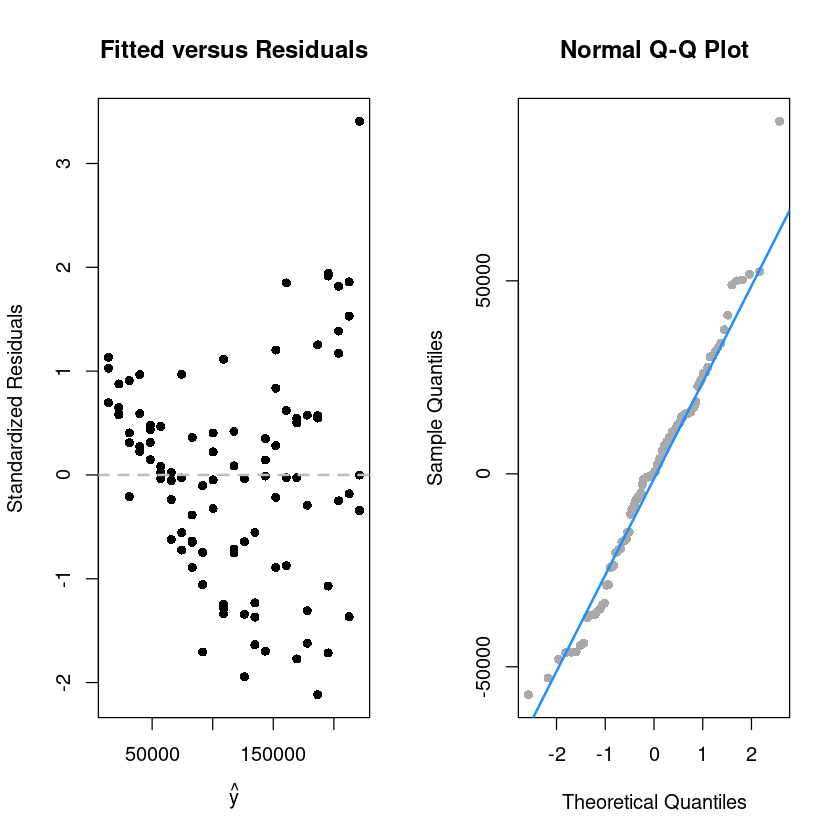

  • 잔차게 넓게 퍼져있음
library(lmtest)
Loading required package: zoo


Attaching package: ‘zoo’


The following objects are masked from ‘package:base’:

    as.Date, as.Date.numeric


dwtest(initech_fit, alternative = "two.sided") 

    Durbin-Watson test

data:  initech_fit
DW = 1.3313, p-value = 0.0004993
alternative hypothesis: true autocorrelation is not 0

  • 등분산성 만족하지 않는다.

  • 변수변환(log y),WLSE -> GLS 를 한다.

hist(resid(initech_fit))

LM2(반응변수 변환)

initech_fit_log = lm(log(salary) ~ years, data = initech) 
summary(initech_fit_log)

Call:
lm(formula = log(salary) ~ years, data = initech)

Residuals:
     Min       1Q   Median       3Q      Max 
-0.57022 -0.13560  0.03048  0.14157  0.41366 

Coefficients:
            Estimate Std. Error t value Pr(>|t|)    
(Intercept) 10.48381    0.04108  255.18   <2e-16 ***
years        0.07888    0.00278   28.38   <2e-16 ***
---
Signif. codes:  0 ‘***’ 0.001 ‘**’ 0.01 ‘*’ 0.05 ‘.’ 0.1 ‘ ’ 1

Residual standard error: 0.1955 on 98 degrees of freedom
Multiple R-squared:  0.8915,    Adjusted R-squared:  0.8904 
F-statistic: 805.2 on 1 and 98 DF,  p-value: < 2.2e-16

  • 로그변환을 한 모형이므로 RMSE가 작다고 엇 작네 하면 안돼 .y를 예측하는 것과 y`을 예측하는것은 다르다.

  • \(log \hat y = \hat y^` = \hat \beta_0 + \hat \beta_1 x_1\)

  • \(\rightarrow \hat y = exp(\hat y^`)\) 역변환 해줘야함

par(mfrow=c(1,2))
plot(log(salary)~years, initech,
        pch=16, cex=1.5)
abline(initech_fit_log, col='darkorange', lwd=2)

plot(salary~years, initech,pch=16, cex=1.5)
lines(initech$years,exp(fitted(initech_fit_log)), col="darkorange", lwd=2)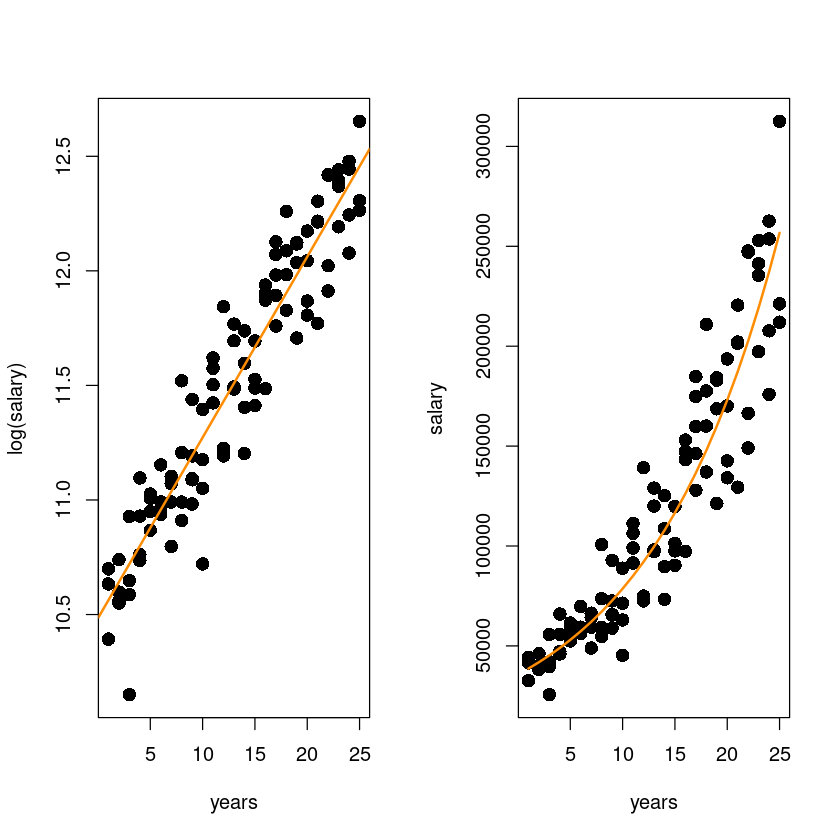

  • 왼쪽 그림: \(\hat y^` = \hat {log y}\)

  • 오른쪽 그림: \(\hat y = exp(\hat \beta_0 + \hat \beta_1x)\)

par(mfrow=c(1,2))

plot(fitted(initech_fit_log), rstandard(initech_fit_log),  pch = 16,
     xlab = expression(hat(y)), 
     ylab = "Standardized Residuals",  
     main = "Fitted versus Residuals")
abline(h = 0, col = "grey", lwd = 2, lty=2)

qqnorm(resid(initech_fit_log), pch=16,
          main = "Normal Q-Q Plot", col = "darkgrey")
qqline(resid(initech_fit_log), col = "dodgerblue", lwd = 2)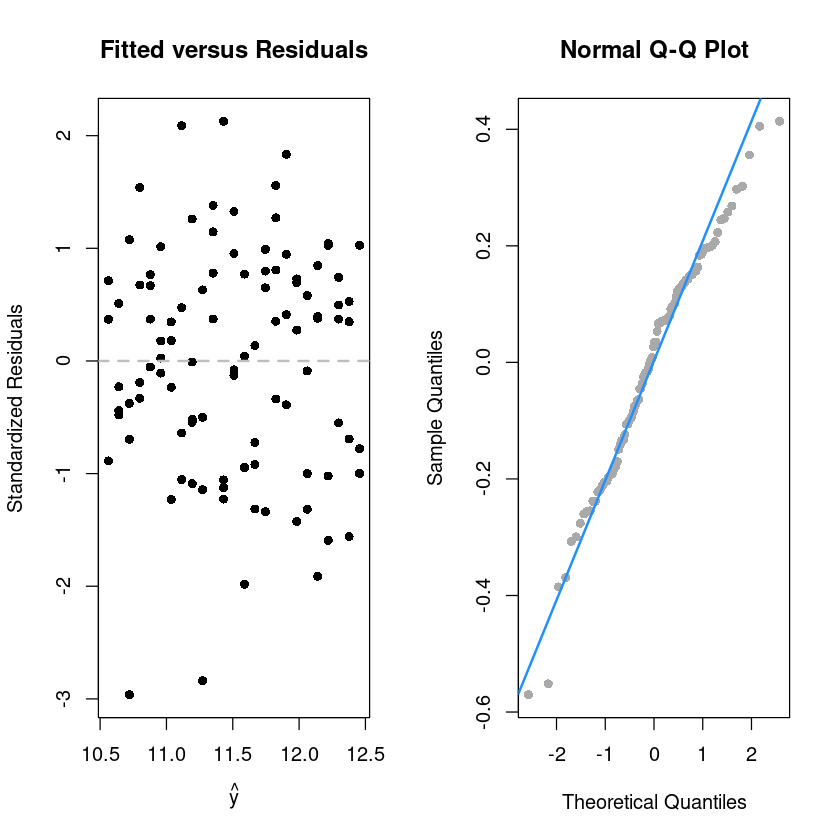

정리

\(y=\beta_0+\beta_x+\epsilon\)

summary(initech_fit)$sigma
27355.0944284452

\(log y = \beta_0+\beta_1x+\epsilon\)

summary(initech_fit_log)$sigma
0.195455087632113
  • 값 작게 나왔다고 더 좋은 모형인거 아님! 변환을 다시 해야함.

\(\sqrt{MSE}=\hat \sigma\) -LM1

sqrt(sum((initech$salary - fitted(initech_fit)) ^ 2)/98)
27355.0944284452

\(\sqrt{MSE}=\hat \sigma\) -LM2

sqrt(sum((initech$salary - exp(fitted(initech_fit_log))) ^ 2)/98)
24526.871988033

\(y-(exp(\hat{log y})=\hat y)\)

  • MSE를 보면 조오금 줄어들었다.

boxcox변환

\(y'=log y\)

log변환은 앞쪽은 작게 압축시키고 뒤쪽은 확 압축시킴

log변환과 다르게 덜 압축하는 방법??? sqrt로 압축..

지수변환 \(\lambda\)파라미터를 이용해서 변환.. (일반화..)

\[y'=g_{\lambda}(y)= \begin{cases} \dfrac{y^{\lambda}-1}{\lambda} & \lambda \neq 0 \\ log y & \lambda=0 \end{cases}\]

library(MASS)
boxcox(initech_fit, plotit = TRUE)

  • (-2,2)가 기본으로 보여줌

  • 0을 좌우로 점선은 \(\lambda\)의 95% 신뢰구간

boxcox(initech_fit, plotit = TRUE, lambda = seq(-0.5,0.5, by = 0.1))

  • log-Likeilihood를 이용하여 가장 큰 \(\lambda\)를 찾아준다.

  • \(\lambda\)를 결정해주는 함수->boxcox

  • 가장 큰 \(\hat \lambda\) 은 0.08… 근데 의미가 없음.. 신뢰구간에 0이 들어가있네? 0은 로그변환이니까 0도 괜찮겠다!