1번

원점을 지나는 회귀모형은 다음과 같이 정의할 수 있다.

\[y_i = β_1x_i + ϵ_i, ϵ_i ∼_{i.i.d.} N(0, σ^2), i = 1, \dots , n\]

(1)

오차제곱합을 정의하고 $β_1$의 최소제곱추정량 $(\hatβ_1)$을 구하여라.

$S=\sum_{i=1}^n \epsilon^2 = \sum_{i=1}^n (y_i-\beta_1 x_i)^2 = \sum(y_i^2 + \beta_1^2 x_i^2 -2 \beta_1 x_i y_i)$

$\widehat \beta_1 = argmin \sum_{i=1}^n(y_i - \beta_1 x_i)^2$

$\dfrac{\partial S}{\partial \beta_1}= -2 \sum_{i=1}^n x_i(y_i-\beta_1 x_i)$

= $\sum x_iy_i - \beta_1 \sum x_i^2 = 0$

$\therefore \widehat \beta_1 = \dfrac{\sum_{i=1}^n x_i y_i}{\sum_{i=1}^n x_i^2}$

(2)

$E(\hatβ_1)$을 구하여라.

$a_i = \dfrac{x_i}{\sum_{i=1}^n x_i^2}$라고 놓자.

즉, $\widehat \beta_1 = \sum_{i=1}^n a_i y_i$

$E(\widehat \beta_1)= E(\sum_{i=1}^n a_i y_i) = \sum_{i=1}^n a_i E(y_i)=\sum_{i=1}^n a_i E(\beta_1 x_i + \epsilon_i)=\sum_{i=1}^n a_i \beta_1 x_i = \dfrac{\sum_{i=1}^n x_i^2}{\sum_{i=1}^n x_i^2} \beta_1 = \beta_1$

$E(\hatβ_1)=\beta_1$이므로 불편추정량

(3)

$Var(\hatβ_1)$을 구하여라.

$Var(\widehat \beta_1)= Var(\sum_{i=1}^n a_i y_i) = \sum_{i=1}^n a_i^2 Var(y_i)=\dfrac{\sigma^2}{\sum_{i=1}^n x_i^2}$

$\because Var(y_i) = \sigma^2$

(4)

제곱합에 대한 분산분석표를 작성하여라.

요인	제곱합(SS)	자유도(df)	평균제곱(MS)	$F_0$	유의확률
회귀	$SSR$	1	$MSR=\dfrac{SSR}{1}$	$\dfrac{MSR}{MSE}$	$P(F \geq F_0)$
잔차	$SSE$	$n-1$	$MSE=\dfrac{SSE}{n-1}$
계	$SST$	$n$

$SSR=\sum_{i=1}^n (\widehat y_i)^2 = \sum (\widehat \beta_1 x_i)^2 = \widehat \beta_1^2 \sum x_i^2$

$SSE=\sum_{i=1}^n(y_i - \widehat y)^2 = \sum(y_i - \widehat \beta_1 x_i)^2 = \sum y_i^2 - SSR$

$SST=SSE+SSR=\sum y_i^2$

절편이 없는 모형은 평균이 0인 느낌

$R^2=\dfrac{\sum \widehat y_i^2}{\sum y_i^2}$

(5)

회귀모형의 유의성 검정을 하기 위한 가설을 설정하고, 검정통계량을 제시하여라.

가설 $H_0: \beta_1 = 0 \ vs \ H_1:\beta_1 \neq 0$
검정통계량 $F=\dfrac{MSR}{MSE}=\dfrac{SSR/1}{SSE/(n-1)} \sim_{H_0} F(1,n-1)$

(6)

위의 가설에 대해, 유의수준 $α$에서 검정하는 방법을 기술하여라.

$F_0 > F_\alpha(1,n-1)$이면 귀무가설을 기각(유의함)하고 그 외는 귀무가설을 채택

혹은,

유의확률 = $P(F>F_0) < \alpha \to H_0$기각

유의확률 = $P(F>F_0) > \alpha \to H_0$기각못함

(7)

다음의 가설에 대한 검정통계량을 제시하고, 유의수준 $α$에서 가설 검정하는 방법을 기술하여라.

\[H_0 : β_1 = 0 \ vs \ H_1 : β_1 > 0\]

검정통계량 $T=\dfrac{\widehat \beta_1 - 0}{\widehat{s.e}(\widehat \beta_1)} \sim_{H_0} t(n-1)$

$s.e(\widehat \beta_1)=\sqrt{Var(\widehat \beta_1)} = \dfrac{\sigma}{\sqrt{\sum x_i^2}}$

$\widehat{s.e}(\widehat \beta_1)= \sqrt{\dfrac{\hat {\sigma^2}}{\sum x_i^2}}, {\hat \sigma^2}=MSE$ $

유의확률 = $P(T > t_0) < \alpha \to H_0$기각

혹은

$t_0>t_{\alpha}(n-1) \to H_0$ 기각

$t_0<t_{\alpha}(n-1) \to H_0$ 기각 못함

2번

‘cars.csv’ 데이터를 이용하여 회귀모형을 적합하려고 한다.

이는 자동차의 속도(mph)에 따른 제동거리(ft)를 조사한 데이터이다.

다음 물음에 답하여라. (R을 이용하여 풀이)(검정에서는 유의수준 $α = 0.05$ 사용)

library(tidyverse)

── Attaching packages ─────────────────────────────────────── tidyverse 1.3.1 ──

✔ ggplot2 3.4.1     ✔ purrr   1.0.1
✔ tibble  3.2.0     ✔ dplyr   1.1.0
✔ tidyr   1.3.0     ✔ stringr 1.5.0
✔ readr   2.1.4     ✔ forcats 1.0.0

── Conflicts ────────────────────────────────────────── tidyverse_conflicts() ──
✖ dplyr::filter() masks stats::filter()
✖ dplyr::lag()    masks stats::lag()

read_csv('cars')

ERROR: Error: 'cars' does not exist in current working directory ('/home/coco/Dropbox/coco/posts/Applied statistics').

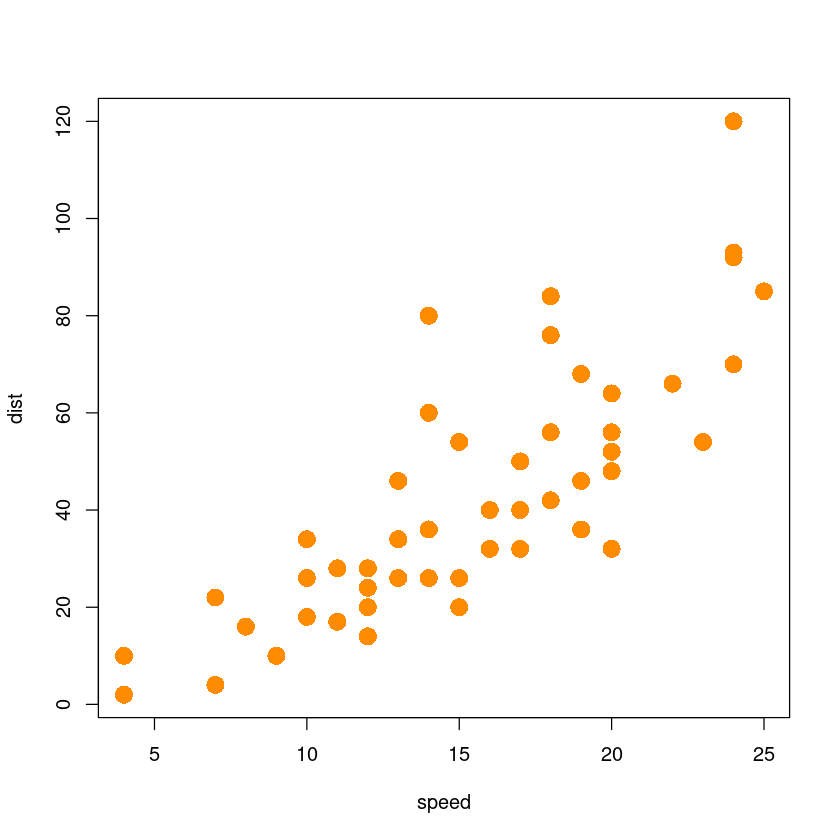
(1) 산점도

이 데이터의 산점도를 그리고 두 변수 사이의 관계를 설명하시오.

plot(dist~speed,
     data=cars,
     xlab="speed",
     ylab="dist",
     pch=16,
     cex=2,
     col="darkorange")

두 변수 사이에 선형관계가 있어 보인다.

(2) 회귀직선

최소제곱법의 의한 회귀직선을 적합시키시키고, 모형 적합 결과를 설명하시오.

dt <- data.frame(
  i = 1:nrow(cars),
  x = cars$speed,
  y = cars$dist,
  x_barx = cars$speed - mean(cars$speed),
  y_bary = cars$dist - mean(cars$dist)) 
dt

A data.frame: 50 × 5
i	x	y	x_barx	y_bary
<int>	<dbl>	<dbl>	<dbl>	<dbl>
1	4	2	-11.4	-40.98
2	4	10	-11.4	-32.98
3	7	4	-8.4	-38.98
4	7	22	-8.4	-20.98
5	8	16	-7.4	-26.98
6	9	10	-6.4	-32.98
7	10	18	-5.4	-24.98
8	10	26	-5.4	-16.98
9	10	34	-5.4	-8.98
10	11	17	-4.4	-25.98
11	11	28	-4.4	-14.98
12	12	14	-3.4	-28.98
13	12	20	-3.4	-22.98
14	12	24	-3.4	-18.98
15	12	28	-3.4	-14.98
16	13	26	-2.4	-16.98
17	13	34	-2.4	-8.98
18	13	34	-2.4	-8.98
19	13	46	-2.4	3.02
20	14	26	-1.4	-16.98
21	14	36	-1.4	-6.98
22	14	60	-1.4	17.02
23	14	80	-1.4	37.02
24	15	20	-0.4	-22.98
25	15	26	-0.4	-16.98
26	15	54	-0.4	11.02
27	16	32	0.6	-10.98
28	16	40	0.6	-2.98
29	17	32	1.6	-10.98
30	17	40	1.6	-2.98
31	17	50	1.6	7.02
32	18	42	2.6	-0.98
33	18	56	2.6	13.02
34	18	76	2.6	33.02
35	18	84	2.6	41.02
36	19	36	3.6	-6.98
37	19	46	3.6	3.02
38	19	68	3.6	25.02
39	20	32	4.6	-10.98
40	20	48	4.6	5.02
41	20	52	4.6	9.02
42	20	56	4.6	13.02
43	20	64	4.6	21.02
44	22	66	6.6	23.02
45	23	54	7.6	11.02
46	24	70	8.6	27.02
47	24	92	8.6	49.02
48	24	93	8.6	50.02
49	24	120	8.6	77.02
50	25	85	9.6	42.02

dt$x_barx2 <- dt$x_barx^2
dt$y_bary2 <- dt$y_bary^2
dt$x_barxy_bary <-dt$x_barx * dt$y_bary
dt

A data.frame: 50 × 8
i	x	y	x_barx	y_bary	x_barx2	y_bary2	x_barxy_bary
<int>	<dbl>	<dbl>	<dbl>	<dbl>	<dbl>	<dbl>	<dbl>
1	4	2	-11.4	-40.98	129.96	1679.3604	467.172
2	4	10	-11.4	-32.98	129.96	1087.6804	375.972
3	7	4	-8.4	-38.98	70.56	1519.4404	327.432
4	7	22	-8.4	-20.98	70.56	440.1604	176.232
5	8	16	-7.4	-26.98	54.76	727.9204	199.652
6	9	10	-6.4	-32.98	40.96	1087.6804	211.072
7	10	18	-5.4	-24.98	29.16	624.0004	134.892
8	10	26	-5.4	-16.98	29.16	288.3204	91.692
9	10	34	-5.4	-8.98	29.16	80.6404	48.492
10	11	17	-4.4	-25.98	19.36	674.9604	114.312
11	11	28	-4.4	-14.98	19.36	224.4004	65.912
12	12	14	-3.4	-28.98	11.56	839.8404	98.532
13	12	20	-3.4	-22.98	11.56	528.0804	78.132
14	12	24	-3.4	-18.98	11.56	360.2404	64.532
15	12	28	-3.4	-14.98	11.56	224.4004	50.932
16	13	26	-2.4	-16.98	5.76	288.3204	40.752
17	13	34	-2.4	-8.98	5.76	80.6404	21.552
18	13	34	-2.4	-8.98	5.76	80.6404	21.552
19	13	46	-2.4	3.02	5.76	9.1204	-7.248
20	14	26	-1.4	-16.98	1.96	288.3204	23.772
21	14	36	-1.4	-6.98	1.96	48.7204	9.772
22	14	60	-1.4	17.02	1.96	289.6804	-23.828
23	14	80	-1.4	37.02	1.96	1370.4804	-51.828
24	15	20	-0.4	-22.98	0.16	528.0804	9.192
25	15	26	-0.4	-16.98	0.16	288.3204	6.792
26	15	54	-0.4	11.02	0.16	121.4404	-4.408
27	16	32	0.6	-10.98	0.36	120.5604	-6.588
28	16	40	0.6	-2.98	0.36	8.8804	-1.788
29	17	32	1.6	-10.98	2.56	120.5604	-17.568
30	17	40	1.6	-2.98	2.56	8.8804	-4.768
31	17	50	1.6	7.02	2.56	49.2804	11.232
32	18	42	2.6	-0.98	6.76	0.9604	-2.548
33	18	56	2.6	13.02	6.76	169.5204	33.852
34	18	76	2.6	33.02	6.76	1090.3204	85.852
35	18	84	2.6	41.02	6.76	1682.6404	106.652
36	19	36	3.6	-6.98	12.96	48.7204	-25.128
37	19	46	3.6	3.02	12.96	9.1204	10.872
38	19	68	3.6	25.02	12.96	626.0004	90.072
39	20	32	4.6	-10.98	21.16	120.5604	-50.508
40	20	48	4.6	5.02	21.16	25.2004	23.092
41	20	52	4.6	9.02	21.16	81.3604	41.492
42	20	56	4.6	13.02	21.16	169.5204	59.892
43	20	64	4.6	21.02	21.16	441.8404	96.692
44	22	66	6.6	23.02	43.56	529.9204	151.932
45	23	54	7.6	11.02	57.76	121.4404	83.752
46	24	70	8.6	27.02	73.96	730.0804	232.372
47	24	92	8.6	49.02	73.96	2402.9604	421.572
48	24	93	8.6	50.02	73.96	2502.0004	430.172
49	24	120	8.6	77.02	73.96	5932.0804	662.372
50	25	85	9.6	42.02	92.16	1765.6804	403.392

colSums(dt)

i: 1275
x: 770
y: 2149
x_barx: -1.77635683940025e-14
y_bary: 1.63424829224823e-13
x_barx2: 1370
y_bary2: 32538.98
x_barxy_bary: 5387.4

$\beta_1 = \dfrac{S_{xy}}{S_{xx}}$

$\beta_0 = \bar y - \beta_1 \bar x$

beta1 <- as.numeric(colSums(dt)[8]/colSums(dt)[6])
beta0 <- mean(cars$dist) - beta1 * mean(cars$speed)
beta1
beta0

3.93240875912409

-17.579094890511

model <- lm(dist~speed, cars)
model


Call:
lm(formula = dist ~ speed, data = cars)

Coefficients:
(Intercept)        speed  
    -17.579        3.932

summary(model)


Call:
lm(formula = dist ~ speed, data = cars)

Residuals:
    Min      1Q  Median      3Q     Max 
-29.069  -9.525  -2.272   9.215  43.201 

Coefficients:
            Estimate Std. Error t value Pr(>|t|)    
(Intercept) -17.5791     6.7584  -2.601   0.0123 *  
speed         3.9324     0.4155   9.464 1.49e-12 ***
---
Signif. codes:  0 ‘***’ 0.001 ‘**’ 0.01 ‘*’ 0.05 ‘.’ 0.1 ‘ ’ 1

Residual standard error: 15.38 on 48 degrees of freedom
Multiple R-squared:  0.6511,    Adjusted R-squared:  0.6438 
F-statistic: 89.57 on 1 and 48 DF,  p-value: 1.49e-12

p-value의 값이 1.49$e^{-12}$로 0.05보다 작아 유의하다.
F검정은 89.57
$\mathbb{R^2}$는 0.6511
$\beta_0, \beta_1$의 p-value값은 유의하다.

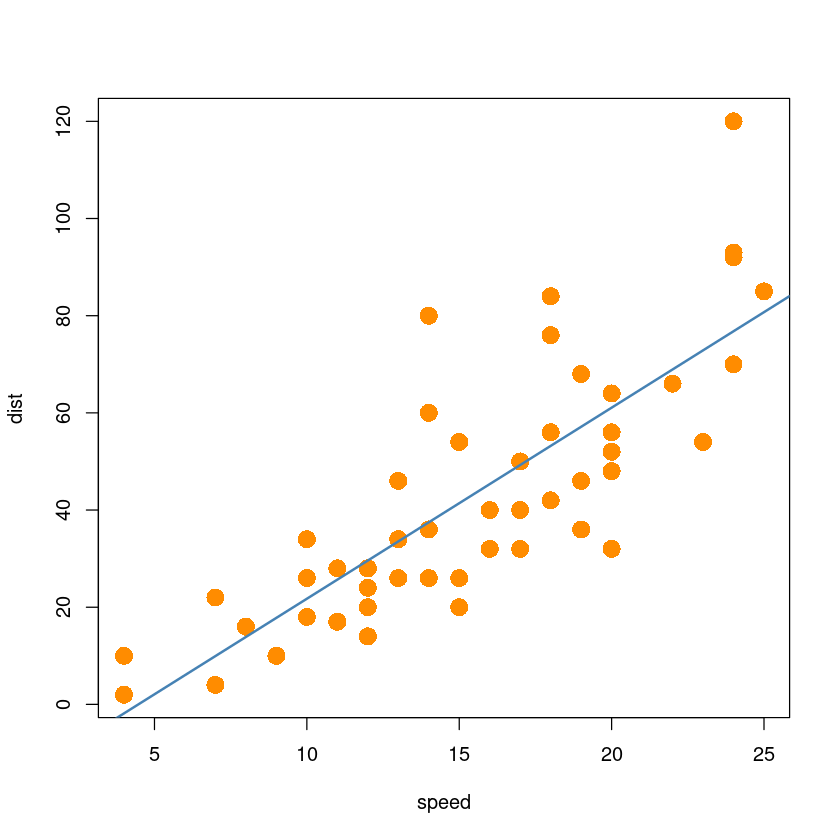
(3) 산점도 위에 회귀직선

데이터의 산점도를 그리고 추정한 회귀직선을 (1)에서 그린 산점도 위에 그리시오.

plot(dist~speed,
     data=cars,
     xlab="speed",
     ylab="dist",
     pch=16,
     cex=2,
     col="darkorange")
abline(model, col='steelblue', lwd=2)

(4) 분산분석

분산분석표를 작성하고 회귀직선의 유의 여부를 검정하시오.

anova(model)

A anova: 2 × 5
	Df	Sum Sq	Mean Sq	F value	Pr(>F)
	<int>	<dbl>	<dbl>	<dbl>	<dbl>
speed	1	21185.46	21185.4589	89.56711	1.489836e-12
Residuals	48	11353.52	236.5317	NA	NA

가정: $H_0: \beta_1 = 0$ vs $H_1: \beta_1 \neq 0$

qf(0.95,1,48)

4.04265212856665

$F_0 > F_{0.05}(0.95,1,48) = 4.04$ 이므로 귀무가설을 기각할 수 잇다. 즉 회귀직선이 유의하다.

(5) 결정계수, 상관계수

결정계수와 상관계수를 구하고 이 둘의 관계를 설명하시오.

$\mathbb{R^2} = \dfrac{SSR}{SST} = \dfrac{21185.46}{32538.98} = 0.651079413060889$

- 결정계수 직접계산

SST = sum((dt$y- mean(dt$y))^2)
SSR = sum(((-17.57909 + 3.932409*dt$x)-mean(dt$y))^2)

SST
SSR

32538.98

21185.4615442987

R2=SSR/SST
R2

0.651079460520848

- 결정계수 코드

summary(model)$r.squared

0.651079380758251

$r_{xy} = \dfrac{S_{xy}}{\sqrt{S{(xx)}S{(yy)}}}$

Sxy <- sum((dt$x - mean(dt$x))*(dt$y - mean(dt$y)))
Sxx <- sum((dt$x - mean(dt$x))^2)
Syy <- sum((dt$y - mean(dt$y))^2)

rxy<-Sxy/sqrt(Sxx*Syy)

rxy**2

0.651079380758251

단순선형회귀모형에서는 표본상관계수와 결정계수가 같다.

$\mathbb{R^2} = r_{xy}^2$

(6) 개별 회귀계수 유의성검정

$β_0, β_1$에 대한 개별 회귀계수의 유의성검정을 수행하시오.

가설 $H_0: \beta_1 = 0$ vs $H_1: not H_0$

- 직접구현

SSE=SST-SSR
MSE=SSE/48

tvalue1 = beta1/(sqrt((MSE/sum((dt$x-mean(dt$x))^2))))
tvalue1

9.46399107202371

tvalue0 = beta0/(sqrt((MSE*((1/48)+((mean(dt$x))^2/sum((dt$x-mean(dt$x))^2))))))
tvalue0

-2.59546417223485

- 코드구현

summary(model)$coef

A matrix: 2 × 4 of type dbl
	Estimate	Std. Error	t value	Pr(>\|t\|)
(Intercept)	-17.579095	6.7584402	-2.601058	1.231882e-02
speed	3.932409	0.4155128	9.463990	1.489836e-12

- 결과

qt(0.975,48)

2.01063475762423

qt(0.025,48)

-2.01063475762423

$\beta_0$에 대한 $t-vlaue$값이 $-2.601058$
$\beta_1$에 대한 $t-vlaue$값이 $9.463990$
$\beta_0, \beta_1$의 t-value는 유의수준 $\alpha=0.05$에서의 $tvalue=-2.011$보다 크기 때문에 유의하다. 즉 귀무가설을 기각한다. $\beta_0, \beta_1$은 모두 0이 아니다.

(7) 개별 회귀계수 신뢰구간

$β_0, β_1$에 대한 90% 신뢰구간을 구하시오.

\[\widehat \beta_0 \pm t_{\alpha/2}(n-2) \widehat \sigma \sqrt{\dfrac{1}{n}+\dfrac{\bar x^2}{S_{xx}}}\]

\[\widehat \beta_1 \pm t_{\alpha/2}(n-2) \dfrac{\widehat \sigma}{\sqrt{S_{xx}}}\]

함수사용

confint(model, level=0.9)

A matrix: 2 × 2 of type dbl
	5 %	95 %
(Intercept)	-28.914514	-6.243676
speed	3.235501	4.629317

직접계산

coef(model) + qt(0.95, 48) * summary(model)$coef[,2]

(Intercept): -6.24367551036937
speed: 4.62931684193222

coef(model) - qt(0.95, 48) * summary(model)$coef[,2]

(Intercept): -28.9145142706524
speed: 3.23550067631595

(8) 평균반응, 신뢰구간

속도가 18.5mph 인 차량의 평균 제동거리를 예측하고, 95% 신뢰구간을 구하시오.

개별 speed = 18,5

new_speed <- data.frame(speed=18.5)

- 코드

model$coefficients[1] + model$coefficients[2]*18.5

(Intercept): 55.1704671532847

predict(model, 
        newdata = new_speed,
        interval = c("confidence"),  #구간추정
        level = 0.95)  ##평균반응

A matrix: 1 × 3 of type dbl
	fit	lwr	upr
1	55.17047	50.08797	60.25296

- 직접계산

- 평균반응 추정량

\[\widehat \mu_0 = \widehat \beta_0 + \widehat \beta_1 x_0\]

mu0 = beta0+beta1*18.5
mu0

55.1704671532847

\[Var(\widehat\mu_0))=\sigma^2(\dfrac{1}{n} + \dfrac{(x_0 - \bar x)^2}{S_{xx}})\]

varmu=((MSE*((1/48)+((18.5-mean(dt$x))^2/sum((dt$x-mean(dt$x))^2)))))
semu=sqrt(varmu)

semu

2.5664989466792

mu0+qt(0.975,48)*semu

60.3307591408838

mu0-qt(0.975,48)*semu

50.0101751656855

(9) 개별반응, 신뢰구간

속도가 18.5mph 인 차량의 개별 제동거리를 예측하고, 95% 신뢰구간을 구하시오.

- 코드

predict(model, newdata = new_speed, 
        interval = c("prediction"),  
        level = 0.95)  ## 개별 y

A matrix: 1 × 3 of type dbl
	fit	lwr	upr
1	55.17047	23.83284	86.5081

- 직접계산

vary0=MSE*(1+(1/48)+(18.5-mean(dt$x))^2/sum((dt$x-mean(dt$x))^2))
vary0

243.118551337083

sqrt(vary0)

15.5922593403613

mu0+qt(0.975,48)*sqrt(vary0)

86.5208057329061

mu0-qt(0.975,48)*sqrt(vary0)

23.8201285736632

qt(0.95,8)

1.8595480375309

(10) 원점 지나는 회귀직선

원점을 지나는 회귀직선을 구하시오.

- 코드

model2 <- lm(dist ~ 0 + speed, cars)
summary(model2)


Call:
lm(formula = dist ~ 0 + speed, data = cars)

Residuals:
    Min      1Q  Median      3Q     Max 
-26.183 -12.637  -5.455   4.590  50.181 

Coefficients:
      Estimate Std. Error t value Pr(>|t|)    
speed   2.9091     0.1414   20.58   <2e-16 ***
---
Signif. codes:  0 ‘***’ 0.001 ‘**’ 0.01 ‘*’ 0.05 ‘.’ 0.1 ‘ ’ 1

Residual standard error: 16.26 on 49 degrees of freedom
Multiple R-squared:  0.8963,    Adjusted R-squared:  0.8942 
F-statistic: 423.5 on 1 and 49 DF,  p-value: < 2.2e-16

$\widehat {dist} = 2.9091 \widehat {speed}$

- 직접계산

beta1_0 <- sum(dt$x * dt$y)/sum((dt$x^2))
beta1_0

2.9091321439371

(11) 원점 지나는 회귀계수 신뢰구간

위 회귀직선에서 회귀계수(기울기)의 90% 신뢰구간을 구하시오.

-코드

confint(model2, level=0.9)

A matrix: 1 × 2 of type dbl
	5 %	95 %
speed	2.67212	3.146144

- 직접계산

colSums(dt)[6] #Sxx

x_barx2: 1370

SSR_0 = sum(((2.909132*dt$x))^2 )

SSE_0 = sum((dt$y - 2.909132*dt$x)^2)

SST_0 = sum(dt$y^2)

MSE_0 = SSE_0/49

sigma_0 = sqrt(MSE_0)

beta1_0 + qt(0.95,49) * sigma_0/sqrt(1370)

3.64560479353767

beta1_0 - qt(0.95,49) * sigma_0/sqrt(1370)

2.17265949433653

 qt(0.95,49)

1.67655089261685

(12) 원점 지난 회귀직선 분산분석

원점을 지나는 회귀직선에 대한 분산분석표를 작성하고, 회귀직선의 유의 여부를 검정하시오.

anova(model2)

A anova: 2 × 5
	Df	Sum Sq	Mean Sq	F value	Pr(>F)
	<int>	<dbl>	<dbl>	<dbl>	<dbl>
speed	1	111949.22	111949.2232	423.4682	9.227817e-26
Residuals	49	12953.78	264.3628	NA	NA

가정: $H_0: \beta_1 = 0$ vs $H_1: \beta_1 \neq 0$

qf(0.95,1,49)

4.03839263368304

$F_0 > F_{0.05}(0.95,1,49) = 4.04$ 이므로 귀무가설을 기각할 수 잇다. 즉 회귀직선이 유의하다.

(13) 원점 지나는 회귀직선 결정계수

원점을 지나는 회귀직선의 결정계수를 구하시오.

- 코드

summary(model2)$r.squared

0.896289305805206

- 직접계산

SSR_0/SST_0

0.896289217112581

(14) 회귀직선 결과 비교

원점을 포함한 회귀직선과 포함하지 않은 회귀직선의 결과를 비교하여라.

summary(model)$r.squared
summary(model2)$r.squared

0.651079380758251

0.896289305805206

원점을 포함한 회귀직선의 R스퀘어값이 더 크므로 model2가 더 좋은 것 같다.

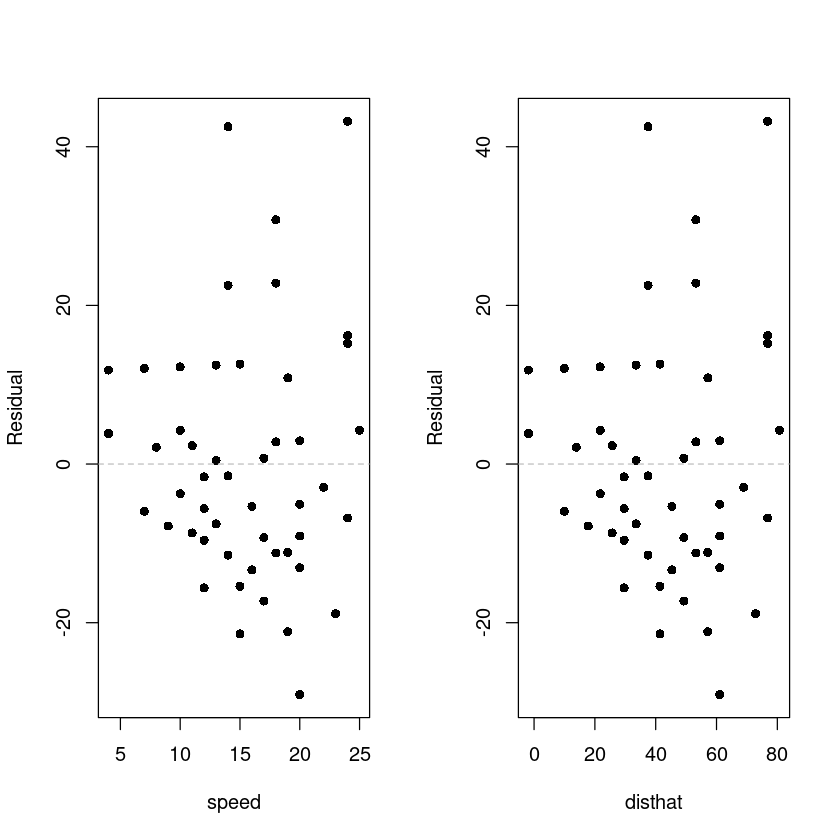
(15) 잔차 산점도

잔차에 대한 산점도를 그리고, 결과를 설명하여라.

cars$disthat <- model$fitted
cars$resid <- model$residuals

par(mfrow=c(1,2))
plot(resid ~ speed, cars, pch=16, ylab = 'Residual')
abline(h=0, lty=2, col='grey')
plot(resid ~ disthat, cars, pch=16, ylab = 'Residual')
abline(h=0, lty=2, col='grey')

(16) 잔차 등분산성 검정

잔차에 대한 등분산성 검정을 수행하시오.

가설:

bptest(model)


    studentized Breusch-Pagan test

data:  model
BP = 3.2149, df = 1, p-value = 0.07297

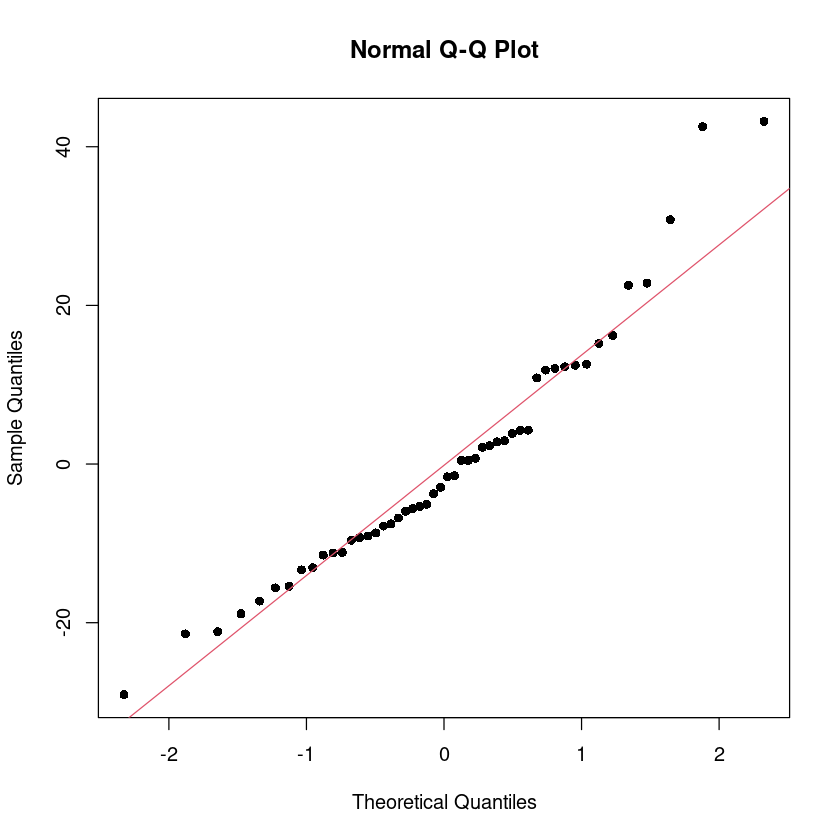
(17) 잔차 정규성 검정

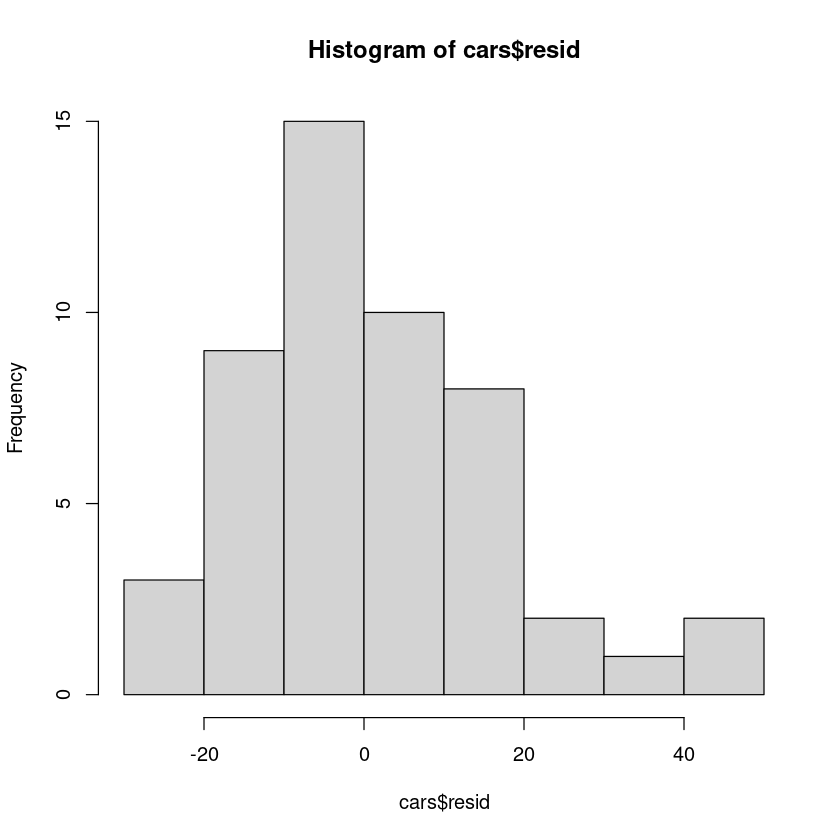
잔차에 대한 히스토그램, QQ plot을 그리고, 정규성 검정을 수행하여라.

가설:

qqnorm(cars$resid, pch=16)
qqline(cars$resid, col=2)

hist(cars$resid)

shapiro.test(resid(model))


    Shapiro-Wilk normality test

data:  resid(model)
W = 0.94509, p-value = 0.02152

$H_0$: 정규성 만족, $H_1$: 정규성만족X
p-value의 값이 0.05 보다 작으므로 귀무가설을 기각

(18) 잔차 독립성 검정

잔차에 대한 독립성 검정을 수행하시오.

dwtest(model, alternative = "two.sided")  #H0 : uncorrelated vs H1 : rho != 0


    Durbin-Watson test

data:  model
DW = 1.6762, p-value = 0.1904
alternative hypothesis: true autocorrelation is not 0

DW TEST의 p-value=0.1904이므로 H0를 기각할 수 없다. 채택. 즉 서로 독립이다.

dwtest(model, alternative = "greater")  #H0 : uncorrelated vs H1 : rho > 0


    Durbin-Watson test

data:  model
DW = 1.6762, p-value = 0.09522
alternative hypothesis: true autocorrelation is greater than 0

dwtest(model, alternative = "less")     #H0 : uncorrelated vs H1 : rho < 0


    Durbin-Watson test

data:  model
DW = 1.6762, p-value = 0.9048
alternative hypothesis: true autocorrelation is less than 0

요인	제곱합(SS)	자유도(df)	평균제곱(MS)	\(F_0\)	유의확률
회귀	\(SSR\)	1	\(MSR=\dfrac{SSR}{1}\)	\(\dfrac{MSR}{MSE}\)	\(P(F \geq F_0)\)
잔차	\(SSE\)	\(n-1\)	\(MSE=\dfrac{SSE}{n-1}\)
계	\(SST\)	\(n\)