AS HW1_

Applied statistics
homework
Author

김보람

Published

April 4, 2023

library(dplyr)
library(lmtest)
Loading required package: zoo


Attaching package: ‘zoo’


The following objects are masked from ‘package:base’:

    as.Date, as.Date.numeric

데이터셋

exams <- read.csv("~/Dropbox/coco/posts/Applied statistics/exams.csv")
head(exams)
A data.frame: 6 × 8
gender race.ethnicity parental.level.of.education lunch test.preparation.course math.score reading.score writing.score
<chr> <chr> <chr> <chr> <chr> <int> <int> <int>
1 female group D some college standard completed 59 70 78
2 male group D associate's degree standard none 96 93 87
3 female group D some college free/reduced none 57 76 77
4 male group B some college free/reduced none 70 70 63
5 female group D associate's degree standard none 83 85 86
6 male group C some high school standard none 68 57 54 
summary(exams)
    gender          race.ethnicity     parental.level.of.education
 Length:1000        Length:1000        Length:1000                
 Class :character   Class :character   Class :character           
 Mode  :character   Mode  :character   Mode  :character           
                                                                  
                                                                  
                                                                  
    lunch           test.preparation.course   math.score     reading.score   
 Length:1000        Length:1000             Min.   : 15.00   Min.   : 25.00  
 Class :character   Class :character        1st Qu.: 58.00   1st Qu.: 61.00  
 Mode  :character   Mode  :character        Median : 68.00   Median : 70.50  
                                            Mean   : 67.81   Mean   : 70.38  
                                            3rd Qu.: 79.25   3rd Qu.: 80.00  
                                            Max.   :100.00   Max.   :100.00  
 writing.score   
 Min.   : 15.00  
 1st Qu.: 59.00  
 Median : 70.00  
 Mean   : 69.14  
 3rd Qu.: 80.00  
 Max.   :100.00  
data <- filter(exams,race.ethnicity== 'group E')
head(data)
A data.frame: 6 × 8
gender race.ethnicity parental.level.of.education lunch test.preparation.course math.score reading.score writing.score
<chr> <chr> <chr> <chr> <chr> <int> <int> <int>
1 female group E associate's degree standard none 82 83 80
2 male group E master's degree free/reduced none 56 46 43
3 female group E associate's degree free/reduced none 80 82 85
4 male group E associate's degree standard none 89 88 86
5 female group E associate's degree standard none 80 79 71
6 female group E some college free/reduced none 69 74 75

- 데이터: Kaggle의 exams 데이터

  • group E의 아래 두 데이터 상관관계를 보고자 함

  • Reading score: The student’s score on a standardized reading test

  • Writing score: The student’s score on a standardized writing test

nrow(data)
ncol(data)
143
8

산점도

dt <- data.frame(
  i = 1:nrow(data),
  x = data$reading.score,
  y = data$writing.score,
  x_barx = data$reading.score - mean(data$reading.score),
  y_bary = data$writing.score - mean(data$writing.score)) 
head(dt)
A data.frame: 6 × 5
i x y x_barx y_bary
<int> <int> <int> <dbl> <dbl>
1 1 83 80 6.384615 4.96503497
2 2 46 43 -30.615385 -32.03496503
3 3 82 85 5.384615 9.96503497
4 4 88 86 11.384615 10.96503497
5 5 79 71 2.384615 -4.03496503
6 6 74 75 -2.615385 -0.03496503 
dt$x_barx2 <- dt$x_barx^2
dt$y_bary2 <- dt$y_bary^2
dt$x_barxy_bary <-dt$x_barx * dt$y_bary
head(dt)
A data.frame: 6 × 8
i x y x_barx y_bary x_barx2 y_bary2 x_barxy_bary
<int> <int> <int> <dbl> <dbl> <dbl> <dbl> <dbl>
1 1 83 80 6.384615 4.96503497 40.763314 2.465157e+01 31.69983862
2 2 46 43 -30.615385 -32.03496503 937.301775 1.026239e+03 980.76277569
3 3 82 85 5.384615 9.96503497 28.994083 9.930192e+01 53.65788058
4 4 88 86 11.384615 10.96503497 129.609467 1.202320e+02 124.83270576
5 5 79 71 2.384615 -4.03496503 5.686391 1.628094e+01 -9.62183970
6 6 74 75 -2.615385 -0.03496503 6.840237 1.222554e-03 0.09144701 

plot(y~x,
     data=dt,
     xlab="reading.score",
     ylab="writing.score",
     pch=16,
     cex=2,
     col="darkorange")

  • 양의 상관관계가 있어 보인다.

회귀직선

model_ <- lm(y~x,dt)
model_

Call:
lm(formula = y ~ x, data = dt)

Coefficients:
(Intercept)            x  
     -2.506        1.012

\(\widehat y =-2.506 + 1.012 x\)

summary(model_)

Call:
lm(formula = y ~ x, data = dt)

Residuals:
     Min       1Q   Median       3Q      Max 
-11.5572  -3.4544   0.3703   3.3341  12.7208 

Coefficients:
            Estimate Std. Error t value Pr(>|t|)    
(Intercept)  -2.5063     2.2880  -1.095    0.275    
x             1.0121     0.0294  34.419   <2e-16 ***
---
Signif. codes:  0 ‘***’ 0.001 ‘**’ 0.01 ‘*’ 0.05 ‘.’ 0.1 ‘ ’ 1

Residual standard error: 4.778 on 141 degrees of freedom
Multiple R-squared:  0.8936,    Adjusted R-squared:  0.8929 
F-statistic:  1185 on 1 and 141 DF,  p-value: < 2.2e-16

plot(y~x,
     data=dt,
     xlab="reading.score",
     ylab="writing.score",
     pch=16,
     cex=2,
     col="darkorange")


abline(model_, col='steelblue', lwd=2)

분산분석

anova(model_)
A anova: 2 × 5
Df Sum Sq Mean Sq F value Pr(>F)
<int> <dbl> <dbl> <dbl> <dbl>
x 1 27045.856 27045.85588 1184.685 1.731866e-70
Residuals 141 3218.969 22.82957 NA NA
  • 가정: \(H_0: \beta_1 = 0\) vs \(H_1: \beta_1 \neq 0\)
qf(0.95,1,141)
3.90825811075366
  • \(F_0 > F_{0.05}(0.95,1,141) = 3.91\) 이므로 귀무가설을 기각할 수 잇다. 즉 회귀직선이 유의하다.

결정계수, 상관계수

summary(model_)$r.squared
0.893639917777383 
Sxy <- sum((dt$x - mean(dt$x))*(dt$y - mean(dt$y)))
Sxx <- sum((dt$x - mean(dt$x))^2)
Syy <- sum((dt$y - mean(dt$y))^2)
rxy<-Sxy/sqrt(Sxx*Syy)
rxy**2
0.893639917777383

개별 회귀계수 유의성 검정

\(β_0, β_1\)에 대한 개별 회귀계수의 유의성검정을 수행하시오.

가설 \(H_0: \beta_1 = 0\) vs \(H_1: not H_0\)

summary(model_)$coef
A matrix: 2 × 4 of type dbl
Estimate Std. Error t value Pr(>|t|)
(Intercept) -2.506277 2.2880027 -1.09540 2.752092e-01
x 1.012084 0.0294046 34.41926 1.731866e-70 
qt(0.975,141)
1.97693148863425

\(\beta_0\)의 t-value= -1.09540 < 1.97693148863425 이므로 귀무가설을 기각할 수 없다.

신뢰구간

confint(model_, level=0.9)
A matrix: 2 × 2 of type dbl
5 % 95 %
(Intercept) -6.2945971 1.282043
x 0.9633983 1.060771

평균반응

reading score가 61.2 인 학생의 평균 wiring score 예측하고, 95% 신뢰구간을 구하시오.

new_score <- data.frame(x=61.2)

- 코드

model_$coefficients[1] + model_$coefficients[2]*61.2
(Intercept): 59.4332934119049 
predict(model_, 
        newdata = new_score,
        interval = c("confidence"),  #구간추정
        level = 0.95)  ##평균반응
A matrix: 1 × 3 of type dbl
fit lwr upr
1 59.43329 58.23874 60.62785

개별 y

reading score가 61.2 인 학생의 개별 wiring score 예측하고, 95% 신뢰구간을 구하시오.

predict(model_, newdata = new_score, 
        interval = c("prediction"),  
        level = 0.95)  ## 개별 y
A matrix: 1 × 3 of type dbl
fit lwr upr
1 59.43329 49.91222 68.95437

잔차

data$yhat <- model_$fitted
data$resid <- model_$residuals
par(mfrow=c(1,2))
plot(resid ~ reading.score, data, pch=16, ylab = 'Residual')
abline(h=0, lty=2, col='grey')
plot(resid ~ yhat, data, pch=16, ylab = 'Residual')
abline(h=0, lty=2, col='grey')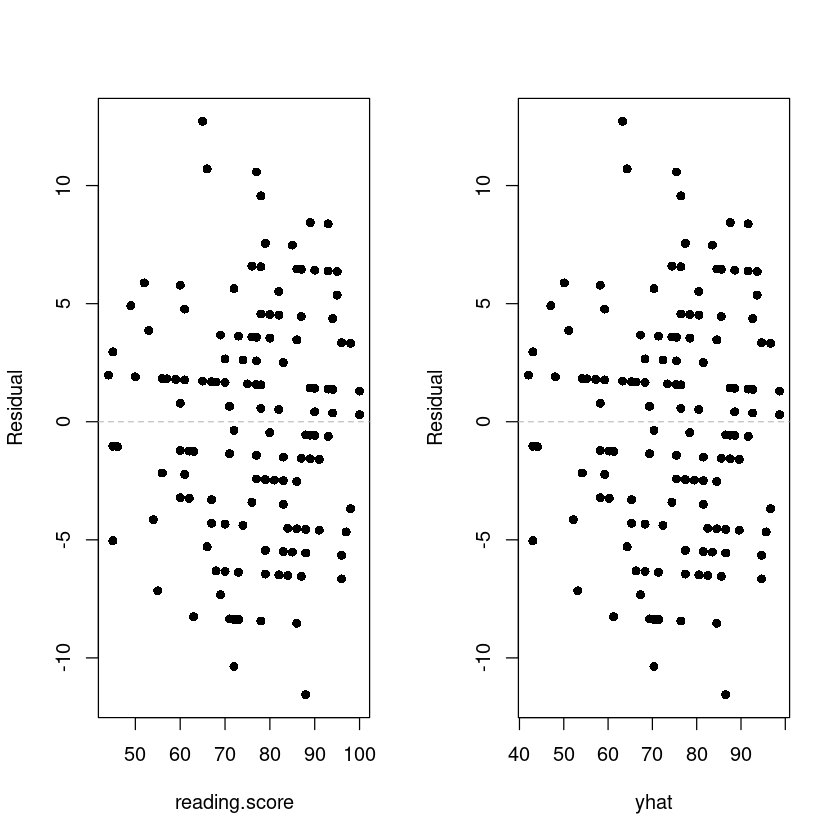

bptest(model_)

    studentized Breusch-Pagan test

data:  model_
BP = 0.057101, df = 1, p-value = 0.8111
qqnorm(data$resid, pch=16)
qqline(data$resid, col=2)
hist(data$resid)

shapiro.test(resid(model_))

    Shapiro-Wilk normality test

data:  resid(model_)
W = 0.9925, p-value = 0.6551

  • \(H_0\): 정규성 만족, \(H_1\): 정규성만족X

  • p-value의 값이 0.05 보다 크므로 귀무가설 채택. 즉 정규성 가정을 만족한다.

dwtest(model_, alternative = "two.sided") 

    Durbin-Watson test

data:  model_
DW = 2.1808, p-value = 0.275
alternative hypothesis: true autocorrelation is not 0
  • H0 : uncorrelated vs H1 : rho != 0

p-value값이 0.275로 0.05보다 크므로 독립성을 먼족한다.