해당 강의노트는 전북대학교 최규빈교수님 AP2023 자료임
칸토어집합
ref: https://en.wikipedia.org/wiki/Cantor_set
정의
- 아래의 집합열 \(C_n\)의 극한 \({\cal C}=\lim_{n\to\infty} C_n\)를 생각하자.
실제수열
- \(C_0=[0,1]\)
- \(C_1=[0,\frac{1}{3}] \cup [\frac{2}{3},1]\)
- \(C_2=\big([0,\frac{1}{9}]\cup[\frac{2}{9},\frac{1}{3}] \big) \cup \big([\frac{2}{3},\frac{7}{9}]\cup [\frac{8}{9},1] \big)\)
- \(\dots\)
언어버전: created by iteratively deleting the open middle third from a set of line segments.
- \(C_0\): \([0,1]\)
- \(C_1\): \(C_0\)에서 정의된 line을 3등분한뒤 가운데를 제거
- \(C_2\): \(C_1\)에서 정의된 line segments를 각각 3등분한뒤 각각 가운데를 제거
- \(\dots\)
수식버전
- \(C_0=[0,1]\)
- \(C_1=\frac{C_{0}}{3}\cup(\frac{2}{3}+\frac{C_{0}}{3})\)
- \(C_2=\frac{C_{1}}{3}\cup(\frac{2}{3}+\frac{C_{1}}{3})\)
- \(\dots\)
- \(C_n=\frac{C_{n-1}}{3}\cup(\frac{2}{3}+\frac{C_{n-1}}{3})\)
단, 여기에서
- \(\frac{1}{3}[a,b]= [\frac{a}{3},\frac{b}{3}]\)
- \(\frac{2}{3}+[a,b]= [\frac{2}{3}+a,\frac{2}{3}+b]\)
와 같이 정의한다.
그림버전

{[0,1]을 3등분해서 [0,1/3], (1/3,2/3), [2/3,1] 로 나누자. 가운데 구간을 날리자.. 이러면서 계속 똑같이 3등분 나누고 반복..
맨 첫번째 집합을 \(C_0\)라고 하면,
\(C_0 = [0,1], C_1 = [0,1/3] \cup [2/3,1], C_2 = [0,1/9] \cup [2/9,1/3] \cup [2/3, 7/9] \cup [8/9,1], \dots\)
성질
- 3진법의 표기: 칸토어 집합의 원소는 \([0,1]\)사이의 원소를 삼진법으로 표현할때 모든 자리수가 0 또는 2가 되는 수만 모은 집합이다.
- \([0,1]\) 사이의 모든 실수를 3진법을 표현한다고 생각하자.
- \(C_1\)은 \(0.1xxxx\dots_{3}\)와 같은 숫자가 빠지고, \(C_2\)에서는 \(0.01xxx\dots_{3}\) 혹은 \(0.21xxx\dots_{3}\) 에 대응하는 숫자가 빠지는 과정이 반복적으로 일어난다고 볼 수 있다.
- 2의 결과를 잘 생각하면 칸토어 집합에 포함되는 수는 삼전법 소수로 표기했을 때 모든 자리수가 0 또는 2가 된다는 점을 쉽게 눈치챌 수 있다.
- 카디널리티: 칸토어 집합의 카디널리티는 구간 \([0,1]\)의 카디널리티와 같다. 즉 \(2^{\aleph_0}\) 이다.
- \(y\in [0,1]\) 사이의 모든 실수는 임의의 2진수로 표현할 수 있다.
- 예를들어 \(y=\frac{3}{5}=0.100110011001..._{2}\)와 같이 표현할 수 있다.
- 만약에 2의 결과에서 \(1\)을 모두 \(2\)로 바꾸어 3진법수를 만들면 \(0.200220022002..._{3}=\frac{7}{10}\)와 같이 쓸 수 있는데, 이는 칸토르 집합의 원소가 된다.
- 3을 2의 출력으로 바꾸는 과정을 수행하는 함수 \(f\)를 정의하자. 즉 이 예제의 경우 \(f(\frac{7}{10})=\frac{3}{5}\).
- \(f\)는 전사함수이므로 \({\sf card}([0,1]) \leq {\sf card}({\cal C})\).
\(card(C) = card([0,1])\)을 보이자
\(C \subset [0,1] \to card(C) \leq card([0,1])\)
WTS: \(card(C) \geq card([0,1])\)
\(f:C \to [0,1]\)인 전사함수(onto) \(f\)가 존재함을 보이자.
\(x\in C\)에 대하여 \(f\)는 아래를 수행
1. \(x=0.200220022002 \dots=\frac{7}{10}\)이다. x는 0,2로만 표현되어 있으므로 C의 원소이다. 여기에서 모든 숫자 2를 1로 바꾼다. 0.10011001001(2진법으로 해석하면 \(y=\frac{3}{5}\)
2. 1에서 바뀐수를 2진수로 해석, y출력ㅡ
\(f(x)=y,f(\frac{7}{10})=\frac{3}{5}\).
전사함수임을 보이기. \(\forall y \in [0,1], \exists x \in C\) s.t \(f(x)=y\)
- 잴 수 있는 집합: \({\cal C} \in {\cal R}\)
- \(C_0,C_1,C_2\dots \in {\cal R}\)
- \({\cal C} = \lim_{n\to \infty} C_n = \cap_{n=0}^{\infty} C_n\) (\(C_0,C_1,C_2,\dots\) 이 감소하는 집합열임을 이용)
- 시그마필드 \({\cal R}\)은 countable intersection에 닫혀있으므로 \({\cal C} \in {\cal R}\)
- 르벡측도값(길이): \(\lambda({\cal C})=0\)이다. 여기에서 \(\lambda\)은 르벡측도이다. 즉 칸토어집합의 길이는 0이다.
- 칸토어 집합을 만드는 과정에서 제외되는 집합의 길이는 순서대로 \(\frac{1}{3}, \frac{2}{9}, \frac{4}{27} \dots\) 이다.
- 이것은 첫째항이 \(\frac{1}{3}\)이고 공비가 \(\frac{2}{3}\)인 등비수열이므로 무한등비급수의 합을 이용하면 제외되는 길이의 합은 \(1\)이 됨을 계산할 수 있다.
\(\lambda(C) = [0,1] - \sum\)매번마다 제외되는 길이 = \(\lambda(C)-1=0\)
- 굉장히 오래전에 만들었던 표
| 집합 | 카디널리티 | 분류 | 르벡메져 |
|---|---|---|---|
| \(\{1,2,3\}\) | 3 | 가산집합 | 0 |
| \(\mathbb{N}\) | \(\aleph_0\) | 가산집합 | 0 |
| \(\mathbb{Z}\) | \(\aleph_0\) | 가산집합 | 0 |
| \(\mathbb{Q}\) | \(\aleph_0\) | 가산집합 | 0 |
| \([0,1]\) | \(2^{\aleph_0}\) | 비가산집합 | 1 |
| \([0,1]\cap \mathbb{Q}\) | \(\aleph_0\) | 가산집합 | 0 |
| \([0,1]\cup \mathbb{Q}\) | \(2^{\aleph_0}\) | 비가산집합 | 1 |
| \([0,1]\cap \mathbb{Q}^c\) | \(2^{\aleph_0}\) | 비가산집합 | 1 |
| \([0,\infty)\) | \(2^{\aleph_0}\) | 비가산집합 | \(\infty\) |
| 비탈리집합 | \(2^{\aleph_0}\) | 비가산집합 | NA |
| 칸토어집합 | \(2^{\aleph_0}\) | 비가산집합 | 0 |
가산집합이면 르벡메저가 0이다.
밀도함수 (density function)
정의
- (정의) \(X\)를 확률공간 \((\Omega, {\cal F}, P)\)에서 정의된 확률변수라고 하고 \(F_X\)를 \(X\)의 분포함수 라고 하자. 만약에 \(F_X\)가 아래와 같은 방식으로 표현된다면 \(f_X\)를 \(X\)를 밀도함수 (density function) 이라고 한다.
\[F_X(x)=\int_{-\infty}^xf_X(y)dy\]
- 저런 표현이 존재하지 않는다면 어쩌지?
- \(F_X(x)\)가 불연속인 경우: 미분 불가능
- \(F_X(x)\)가 연속인 경우: 미분가능할 수도 있고, 아닐 수도 있고
다양한 밀도함수 예시
- 교양: 함수 \(F_X(x)\)가 연속인 경우는 연속확률변수 \(X\)의 분포함수 (distribution fucntion) 혹은 CDF라고 하고 함수 \(F_X(x)\)가 jump만 존재하는 불연속인 경우는 이산확률변수의 분포함수 (distribution function) 혹은 CDF라고 한다.
(예제1) – 균등분포
아래와 같은 distribution function \(F_X\)을 가지는 확률변수 \(X\)를 고려하자.
\[F_X(x) = \begin{cases} 0 & x<0\\ x & 0\leq x \leq 1 \\ 1 & 1<x\end{cases}\]
이러한 함수 \(F_X\)의 density가 존재하는가?
체크: 일단 \(F_x(x)\)는 (1) 비감소하며 (2) \(\lim_{x\to -\infty}F_X(x) = F_X(0) = 0\), \(\lim_{x\to \infty}F_X(x) = F_X(1) = 1\) (3) 오른쪽연속 (그냥 연속임) 이므로 분포함수의 정의를 만족한다. 따라서 \(F_X(x)\)에 대응하는 확률변수 \(X\)가 있다.
(해설)
- 대충 생각하면 (진짜 말 그대로 대충) 아래와 같이 생각할 수 있다.
\[f_X(x) = \frac{d}{dx}F_x(x)\]
- 즉 \(f_X(x)\)는 \(F_x(x)\)의 도함수 같은 것으로 생각할 수 있다.
- 문제는 \(F_X(x)\)는 연속이지만 \(x=0\)과 \(x=1\)에서 미분가능하지는 않다는 점이다.
- 그래서 \(F_X(x)\)는 미분가능하지 않다.
- 하지만 미분가능의 개념을 “함수”에 적용하는 것이 아니라 “하나의 포인트”에 적용한다면 어떨까?
- \(F_X(x)\)는 \(x=0\)과 \(x=1\)을 제외한 모든 점에서 미분가능하며 그 도함수는 대략적으로 아래와 같이 표현할 수 있다.
\[f_X(x) = \begin{cases} 0 & x<0 \\ ?? & x=0 \\ 1 & 0<x<1 \\ ?? & x=1 \\ 0 & 1<x \end{cases}\]
- 어차피 유한개의 점을 제외하여도 적분값에 영향이 없으므로 ??의 값은 아무값이나 넣어도 상관없다. 편의상 아래와 같은 \(f_X(x)\)를 고려하자.
\[f_X(x) = \begin{cases} 1 & 0\leq x \leq 1 \\ 0 & o.w. \end{cases}\]
- 위와 같은 \(f_X(x)\)에 대하여 아래식이 성립한다고 볼 수 있다. \[F_X(x) = \int_{-\infty}^x f_X(y)dy\]
\(F_X(x)\)는 미분불가능하지만 또 어떠한 의미에서는 가능하다고 볼 수 도 있다.


그림2: 위키에서 긁어온 균등분포의 pdf, cdf 그림. 실제로는 \(x=0,1\)에서 \(F_X'(x)\)의 값이 존재하지 않으나 편의상 정의함.
(예제1의 정답에 대한 의문)
만약에 누군가가 아래와 같은 \(f_X(x)\)들이 pdf라고 주장한다면?
- \(f_X(x) = \begin{cases} 1 & 0< x <1 \\ 0 & o.w. \end{cases}\)
- \(f_X(x) = \begin{cases} 1 & 0\leq x < 1 \\ 0 & o.w. \end{cases}\)
- \(f_X(x) = \begin{cases} 1 & 0< x \leq 1 \\ 0 & o.w. \end{cases}\)
별로 상관없을듯 하다. 어차피 \(\lambda(\{0\})=\lambda(\{1\})=0\) 이므로 넓이에 영향이 없다. 위의 함수는 \(x=0,1\)을 제외한 모든곳에서는 함수값이 일치하므로 거의 같다고 보아도 무방하다. 즉 아래의 함수들은 거의 모든 곳에서 같다. (w.r.t 르벡메저)
- \(f_X(x) = \begin{cases} 1 & 0< x <1 \\ 0 & o.w. \end{cases}\)
- \(f_X(x) = \begin{cases} 1 & 0\leq x < 1 \\ 0 & o.w. \end{cases}\)
- \(f_X(x) = \begin{cases} 1 & 0< x \leq 1 \\ 0 & o.w. \end{cases}\)
- \(f_X(x) = \begin{cases} 1 & 0\leq x \leq 1 \\ 0 & o.w. \end{cases}\)
여기에서 두 함수 \(f\), \(g\)가 거의 모든 곳에서 같다라는 표현은
\[\lambda\big(\{x: f(x) \neq g(x)\}\big)=0\]
을 의미한다. 즉 함수값이 다른 집합의 르벡측도값이 0이라는 의미이다.
(예제2) – 혼합된 균등분포
아래와 같은 distribution function \(F_X\)을 가지는 확률변수 \(X\)를 고려하자.
\[F_X(x) = \begin{cases} 0 & x<0\\ \frac{3}{2}x & 0\leq x < \frac{1}{2} \\ \frac{1}{2}+\frac{1}{2}x & \frac{1}{2}\leq x<1 \\ 1 & 1\leq x\end{cases}\]
이러한 함수 \(F_X\)의 density가 존재하는가?
체크: 일단 \(F_x(x)\)는 (1) 비감소하며 (2) \(\lim_{x\to -\infty}F_X(x) = F_X(0) = 0\), \(\lim_{x\to \infty}F_X(x) = F_X(1) = 1\) (3) 오른쪽연속 (그냥 연속임) 이므로 분포함수의 정의를 만족한다. 따라서 \(F_X(x)\)에 대응하는 확률변수 \(X\)가 있다.
(해설)
함수 \(F_X(x)\)는 \(x=0,\frac{1}{2},1\) 에서 미분불가능하지만 어차피 미분불가능한 점이 countable 하므로 여기에서는 무시하고 \(f_X(x)\) 값을 편의상 정의하여도 무방하다. 따라서 아래와 같은 함수 \(f_X(x)\)가 pdf가 될 수 있다.
\[f_X(x) = \begin{cases} \frac{3}{2} & 0 \leq x <\frac{1}{2} \\ \frac{1}{2} & \frac{1}{2}< x < 1 \end{cases}\]
그 외에도 \(x=0,\frac{1}{2}, 1\)에서의 함수값을 어떻게 정의하느냐에 따라서 여러개의 정답이 있을 수 있지만, 그러한 함수들은 \(f_X(x)\)와 거의 모든 곳에서 같은 함수이다.
여기서도 \(F_X(x)\)는 미분불가능하지만 또 어떠한 의미에서는 가능하다고 볼 수 도 있다.
- 주장: \(F_X(x)\)가 모든 곳에서 연속 이고 거의 모든 곳에서 미분가능하다고 가능하면 아래를 만족하는 (도함수 비스무리한) \(f_X(x)\)가 존재한다.
\[F_X(x) = \int_{-\infty}^{x} f_X(x) dx\]
이때 \(F_X(x)\)가 미분가능하지 않은 집합에 대하여서는 적분을 정의함에 있어서 제외하고 정의해도 무방하다.
엄청 그럴듯해보이지만 칸토어함수의 존재로 인하여 이 주장은 틀렸다.
칸토어함수, 칸토어분포
- 아래와 같은 과정으로 얻어지는 함수 \(F_0, F_1, F_2, \dots\)를 고려하자.
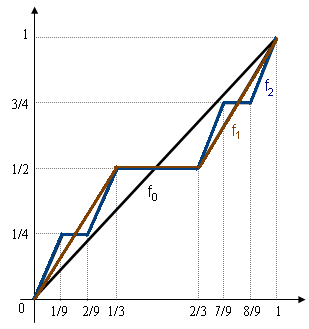
그림에서는 \(f_0, f_1, f_2\) 와 같이 표현하였지만 우리는 편의상 \(F_0, F_1, F_2\)와 같이 표현하도록 하겠다.
\(f_0:[0,1] \to [0,1]\)
\(C_0:[0,1]\)에서 양의 기울기를 가짐
\(f_1:[0,1] \to [0,1]\)
\(C_1\)에서 양의 기울기를 가짐
\([0,1]-C_1\)에서 기울기가 0임
\(f_2:[0,1] \to [0,1]\)
\(C_2\)에서 양의 기울기를 가짐
\([0,1]-C_2\)에서 기울기가 0임
\(F_0, F_1, F_2 \rightarrow\) 분포함수의 정의를 만족! 증가함수이고, 연속이고(오른쪽으로 연속이고), 극한으로 보내면 얼마고..
- 이제 이러한 함수의 극한을 \(F\)라고 하자. 즉
\[F(x) = \lim_{n\to \infty} F_n(x)\]
이다. 이것을 기호로 간단하기 \(F_n \to F\) 와 같이 표현하기도 한다. 여기에서 \(F_n \to F\)의 의미는 \(F_n\)의 임의의 고정된 점 \(x^\star\)에 대하여 \(F_n(x^\star) \to F(x^\star)\)라는 의미이다.
- 함수 \(F_n\)의 정의역을 칸토르 집합 \({\cal C}\)와 연계하여 이해하면 아래와 같은 사실을 관찰할 수 있다.
- \(F_0\)은 \(C_0\)에서는 양의 기울기를 가지고 \([0,1]-C_0\) 에서는 기울기가 0이다.
- \(F_1\)은 \(C_1\)에서는 양의 기울기를 가지고 \([0,1]-C_1\) 에서는 기울기가 0이다.
- \(F_2\)은 \(C_2\)에서는 양의 기울기를 가지고 \([0,1]-C_2\) 에서는 기울기가 0이다.
따라서 아래의 사실을 유추할 수 있다.
- \(F\)는 \({\cal C}\)에서는 양의 기울기를 가지고 \([0,1]-{\cal C}\) 에서는 기울기가 0이다.
- 함수 \(F\)를 칸토어 함수라고 부른다. 칸토어함수는 아래와 같은 특징이 있다.
- 칸토어 함수는 모든 곳에서 연속이다.
- 칸토어 집합의 외부 \([0,1]-{\cal C}\)에서는 상수함수이다. 즉 칸토어집합의 외부에서는 기울기가 0이다. \(m({\cal C})=0\) 이므로 이 함수는 거의 모든 곳에서 기울기가 0이다.
- \(F\)는 비감소함수이다. (감소하지 않는 함수: non-decreasing)
증가하는 길이가 0이네?? 증가할 확률이 0이라고 이해하자. 그런데 0부터 1까지 분명 증가를 했는데.. jump구간이 있나? (잉 1번에서 연속이라고 했는뎁.)
- \(F(0)=0\) 이고 \(F(1)=1\)이다.
특3,4를 하면 분포함수의 정의를 만족하게 된다. 이것을 바탕으로 \(F_x\)확률변수가 존재한다..
- 1,3,4에 의하여 \(F\)는 분포함수의 정의를 만족한다. 1에 의하여 \(F\)는 연속형확률변수의 분포함수가 된다. 칸토어 집합의 외부에서 (그러니까 [0,1]의 거의 모든 점에서) 도함수는 \(0\) 이므로
\[\frac{d}{dx}F(x)=f(x)=0,\quad \sf{a.e.}\]
이다. 하지만 \(f(x)\)는 pdf의 정의를 만족하지 않는다.
- 요약
- 칸토어함수 \(F\)는 분포함수의 정의를 만족한다. 따라서 \(F\)에 대응하는 확률변수 \(X\)가 반드시 있다.
- 심지어 칸토어함수는 연속함수이므로, \(F\)에 대응하는 확률변수 \(X\)는 연속형 확률변수가 된다.
- \(F\)는 거의 모든 점에서 도함수가 존재하지만 그 도함수의 적분이 아니다.
- 그래서 \(X\)의 pdf는 존재하지 않는다.
칸토어함수는 미적분학의 기본정리 성립하지 않는 반례를 찾기 위해 고안되었다. 즉 어떠한 함수 \(F\)가 거의 모든 곳에서 미분가능하며, 그 도함수를 \(f\)가 르벡적분 가능 할지라도 \(\int_{-\infty}^{x} f(y) dy= F(x)\) 가 성립하지 않을 수 있다.
절대연속
- 모티브
- \(F_X\)의 “도함수 비슷한 함수”를 일반화 할 수 없을까? \(\Rightarrow\) 라돈니코딤 도함수
- \(F_X\)의 1과 같이 도함수 비슷한 함수가 언제 존재하는지 조건을 알 수 있을까? \(\Rightarrow\) 절대연속
| 함수 | 도함수 | 라돈니코딤 도함수1 |
|---|---|---|
| 연속 | X | X2 |
| 절대연속 | X | O |
| 미분가능 | O | O |
미분가느앟면 절대연속이고, 절대연속이면 연속이다.
암기: 절대연속은 연속보다 강하고, 미분가능보다 약한 조건이다.
절대연속: 1. 함수버전:def가 어려움 이해가 어렵다., 2. 메저(msr) 버전:def가 쉬움ㅡ
함수버전의 절대연속 def을 일반화하면, msr ver 절대연속의 def가 된다.
\(F_x\)가 분포함수의 범위를 만족한다고 가정하고 \(\mu_x\)가 msr ver 절대연속을 만족하는지 체크하고 \(F_x\)도 함수버전의 절대연속을 만족하는지 체크..
- 함수ver def (\(F_x\)에 한정)
- 정의: 함수 \(F_X(x)\)가 분포함수의 정의를 만족한다고 가정하자.3 \(F_X(x)\)에 대응하는 분포 \(\mu_X:{\cal R} \to [0,1]\)를 생각하자. \(F_X(x)\)가 절대연속이라는 뜻은 아래가 성립한다는 의미이다.
\[\forall B \in {\cal R}: \lambda(B) =0 \Rightarrow \mu_X(B)=0\]
borrel set: B
이럴 경우 아래와 같이 표현한다.
- A measure \(\mu_X\) is abosolutely continous with respect to Lebesgue measure \(\lambda\)
- \(\mu_X << \lambda\) absolutely continuous 기호표현, 또는 \(\lambda\)가 \(\mu_x\)를 dominating 한다고도 표현
\(\lambda(B)\): 구간 B의 길이
\(\mu(B)\):구간 B에서 \(F_X\)의 차이
\(F_X\)가 절대연속이다.
- msr ver def
- 정의: 좀 더 일반적으로는 아래와 같이 정의할 수 있다. [@durrett2019probability, p 470]
가측공간 \((\mathbb{R},{\cal R})\)를 고려하고 \(\mu\), \(\lambda\)를 \((\mathbb{R},{\cal R})\)에서의 메져라고 하자. \(\mu\)가 absolutely continuous w.r.t. \(\lambda\) 라는 의미는
\[\forall B \in {\cal R}:~ \lambda(B) =0 \Rightarrow \mu(B)=0\]
라는 의미이며 기호로는 \(\mu << \lambda\) 와 같이 나타낸다.
\(\mu\)는 \(\lambda\)에 대하여 \((\mathbb{R},{\cal R})\)에서 절대 연속이다.
여기에서 공간 \((\mathbb{R},{\cal R})\) 은 이해를 돕기위해서 제한한 것이며, 대부분 교재에서는 좀 더 일반적인 가측공간에서 절대연속을 정의한다.
- 절대연속의 예제를 살펴보기전에 필요한 예비학습
이런게 있었거든요.. // 7주차 강의노트
함수 \(\mu\)가 잴 수 있는 공간 \((\Omega, {\cal F})\)에서 정의된 메져라고 하자.
- \(A_i \uparrow A\) \(\Rightarrow\) \(\mu(\lim_{n\to \infty}A_n) = \lim_{n \to \infty}\mu(A_n)\)
\(A_i \uparrow A\) 뜻: \(A_1 \subset A_2 \subset A_3 \subset \dots A_i \in {\cal F}\) and \(\cup_{i=1}^\infty A_i = A\)
\(A_i\)가 증가하는 집합열이면, \(\cup_{i=1}^\infty A_i = A\) 이 표현은, \(lim_{n \to \infty} A_n = A\)로 쓸 수 있다.
\(\mu(\lim_{n\to \infty}A_n) = \mu(\cup_{n=1}^\infty A_n)\) : \(A_n\)이 증가하는 집합열이므로 등호가 성립.
\(\mu(\cup_{n=1}^\infty A_n)=\mu(\uplus_{n=1}^\infty B_n)\) : 시그마필드에서 정의되서 가능, 차집합에 닫혀있으므로 가능 (반쯤 닫혀있어서 disjoint)성립!
\(\mu(\uplus_{n=1}^\infty B_n)=\sum_{i=1}^\infty \mu(B_n)\) : msr의 정의: add
\(\sum_{i=1}^\infty \mu(B_n)= lim_{n \to \infty} \sum_{k=1}^n \mu(B_k)=lim_{n \to \infty} \mu (\uplus_{k=1}^\infty B_k)\): msr의 정의: add
\(lim_{n \to \infty} \mu (\uplus_{k=1}^\infty B_k) = lim_{n \to \infty} \mu (\cup_{k=1}^n A_k)\) 위에서 반대 성립햇은게
\(lim_{n \to \infty} \mu (\cup_{k=1}^n A_k)=lim_{n \to \infty} \mu(A_n)\) : \(A_i\)가 증가하는 집합열이므로
- \(A_i \downarrow A\) with \(\mu(A_1)<\infty\) \(\Rightarrow\) \(\mu(\lim_{n\to \infty}A_n) = \lim_{n \to \infty}\mu(A_n)\)
\(A_i \downarrow A\) 뜻 \(A_1 \supset A_2 \supset \dots, A_i \in {\cal F}, \cap_{n=1}^\infty A_n = A\)
\(A_i\)가 감소하는 집합열이므로, \(\cap_{n=1}^\infty A_n = A\) 이 표현은, \(inf \{A_1, A_2, \dots \}=lim_{n \to \infty} A_n= \cap_{i=1}^n A_i=A\)
\(A_i\)가 감소하는 집합열이므로 \(A_1 \cap A_2 = A_2\), \(A_1 \cap A_2 \cap A_3 = A_3, \dots A_1 \cap A_2 \cap \dots = lim A_n\)
\(A_1 \supset A_2 \supset \dots, A_i \in {\cal F}, \cap_{n=1}^\infty A_n = A\) 이 감소하는 열을 증가하는 열로 바꿔보자.
\(A_1 - A_1 \subset A_1-A_2 \subset A_1-A_3 \subset \dots A_1 - A_i \in {\cal F}, \cup_{n=1}^\infty(A_1-A_n)=A_1-A_n\)
증가열에 대해서는 다음과 같은 표현을 쓸 수 있다.
\(\mu(lim_{n \to \infty} (A_1-A_n))=lim_{n \to \infty} \mu(A_1-A_n)\)
LHS: \(\mu(lim_{n \to \infty} (A_1-A_n))\) 이식을 풀어쓰면, \(\mu (A_1 - lim_{n \to \infty} A_n) = \mu(A_1-A)=\mu(A_1)-\mu(A)\)
RHS: \(lim_{n \to \infty} \mu(A_1-A_n)\) 이식을 풀어쓰면, \(lim_{n \to \infty} \{\mu(A_1) - \mu(A_n) \}=\mu(A_1) - lim_{n \to \infty} \mu(A_n)\)
LHS와 RHS를 정리하면, \(\mu(A_1)-\mu(A)=\mu(A_1) - lim_{n \to \infty} \mu(A_n)\) 이므로
\(\mu(A)= lim_{n \to \infty} \mu(A_n)\)이고, \(\mu(A) = \mu(lim_{n \to \infty} A_n)\)
- 감소하거나 증가하는 집합열에서는 \(\lim\)을 넣거나 뺼 수 있다. (정확하지 않은 state, 그냥 기억을 위한 문장)
- 예시
\((\mathbb{N},2^{\mathbb{N}})\) 잴수 있는 공간을 만들고, 이 공간에서 counting msr(\(2^{\mathbb{N}} \to [0,\infty])\)를 정의하자.
\(A_n = \{n, n+1, n+2, \dots \}\) 로 놓자.
\(A_1= \mathbb{N}, A_2 = \mathbb{N} - \{1\} = \{2,3,4,\dots\}, A_3 = \mathbb{N} - \{1,2\} = \{3,4,5,\dots, \}\)
체크할것
1. \(lim_{n \to \infty} A_n = \emptyset\)
2. \(\forall n \in \mathbb{N}: A_n \neq \emptyset\)
위 1,2가 성립된다. 예시의 예시 \(lim_{n \to \infty} \frac{1}{n}=0, \forall n: \frac{1}{n}>0\)
\(A_n \downarrow \emptyset\)이다. \(\rightarrow \#(lim_{n \to \infty}A_n) = lim_{n \to \infty} \#(A_n)\)
LHS는 \(\#(lim_{n \to \infty}A_n) = \#(\emptyset) = 0\), RHS는 \(\infty\)이므로 좌변 우변은 같지 않다.
- 예제1: – 베르누이
아래와 같은 함수를 고려하자.
\[F_X(x) = \begin{cases} 0 & x<0 \\ \frac{1}{2} & 0\leq x< 1 \\ 1 & x \geq 1 \\ \end{cases}\]
질문: \(F_X\)가 절대 연속인가?ㅡ
미분가능 -> 절대연속 -> 연속
연속X -> 절대연속 X
\(F_X\)는 절대연속이 아니다.
이 함수는 르벡메져에 대하여 absolutely continuous 하지 않다.
(해설1)
연속이 아니므로 절대연속이 아니다.
\(\forall B \in {\cal R}: \lambda(B)=0 \rightarrow \mu_X(B)=0\) - (*)
추측: \(B=\{0\}, B=\{1\}\)인 경우는 (*)가 성립하지 않는다.
\(B=\{0\}\)으로 생각하면 \(\rightarrow \lambda(B)=0. \mu_X(B) \neq 0\)일듯!
\(\mu_x(\{0\})\)
\(\{0\} = lim_{n \to \infty}(0-\frac{1}{n},0]\): 감소하는 집합열이므로 \(\cap_{n=1}^\infty [-\frac{1}{n},0]\)
\(\{0\} \in \cap_{n=1}^\infty (-\frac{1}{n},0]\)
\(x<0 \rightarrow \{x\} \not \in \cap_{n=1}^\infty (-\frac{1}{n},0]\): 아무리 0에 가까운 \(x\)라도 그것보다 더 0에 가까운 \(-\frac{1}{n}\)이 존재하므로 그러한 \(-\frac{1}{n}\)에 대해서는 \(x \not \in (-\frac{1}{n},0]\)
\(\mu_x(\{0\}) = \mu_X(lim_{n \to \infty}(-\frac{1}{n},0])=lim_{n \to \infty} \mu_X((-\frac{1}{n},0])\)
\(\mu_X((a,b])=F_X(b)-F_X(a)\)
\((a,b] = (-\infty, b] - (-\infty, a]\)
\(\rightarrow \mu_((a,b])=\mu((-\infty, b] - (-\infty, a])\)
\(\because (-\infty, b] \supset (-\infty, a]\)
\(=\mu((-\infty, b])-\mu( (-\infty, a])=F_X(b)-F_x(a)\)
\(\therefore \mu_X((-\frac{1}{n},0]) = F_X(0)-F_X(-\frac{1}{n})\)
\(lim_{n \to \infty} \mu_X((-\frac{1}{n},0])=F_X(0)-F_X(-\frac{1}{n})=\frac{1}{2}-lim_{n \to \infty}F_X(-frac{1}{2})=\frac{1}{2}-0=\frac{1}{2}\)
(해설2) 위의 파란색 글씨 요약
임의의 \(\{x\}\)에 대하여 \(\mu_X(\{x\})\)를 계산하기 위해서는 아래와 같이 하면 된다.
- \(\mu_{X}(\{x\})=\mu_{X}\big(\lim_{n\to\infty}(x-\frac{1}{n},x]\big)=\lim_{n\to\infty}\mu_{X}\big((x-\frac{1}{n},x]\big)\)
- \((x-\frac{1}{n}, x]= (-\infty, x] - (-\infty,x-\frac{1}{n}]\)
- \(\mu_{X}\big((x-\frac{1}{n},x]\big)=F_X(x)-F_X(x-\frac{1}{n})\)
- \(\mu_{X}(\{x\})=F_X(x)-\lim_{n\to\infty}F_X(x-\frac{1}{n})\)
이를 이용하면
- \(\lambda(\{0\})=0 \not \Rightarrow \mu_X(\{0\})=F_X(0)-\lim_{n\to\infty}F_X(-\frac{1}{n})=\frac{1}{2}-0\)
- \(\lambda(\{1\})=0 \not \Rightarrow \mu_X(\{1\})=F_X(1)-\lim_{n\to\infty}F_X(1-\frac{1}{n})=1-\frac{1}{2}\)
- \(\lambda(\{0,1\})=0 \not \Rightarrow \mu_X(\{0,1\}) =\mu_X(\{0\})+\mu_X(\{1\})=1\)
위에서 언급한 경우 이외에서는 연속임. \(\lambda(\{0.77\})=0 \Rightarrow \mu_X(\{0.77\})=F_X(0.77)-\lim_{n\to\infty}F_X(0.77-\frac{1}{n})=\frac{1}{2}-\frac{1}{2}\)
- 예제2: – 균등분포
아래와 같은 함수를 고려하자.
\[F_X(x) = \begin{cases} 0 & x<0 \\ x & 0\leq x \leq 1 \\ 1 & x> 1 \\ \end{cases}\]
이 함수는 르벡메져에 대하여 absolutely continuous 하다.
연속형 확률변수의 cdf
(해설)
\(F_X\)가 절대연속이어야 도함수 비스무리한게 되니까 절대연속인걸 따지자.
\(\forall B \in {\cal R}: \lambda(B)=0 \rightarrow \mu_X(B)=0\) 을 따지자
\(B\)가 \(x<0\)과 \(x>1\)인 부분에서 선택하자. 그러면 \(\mu_X(B)=0\)
\(B\)가 \(0 \leq x \leq 1\)에서 선택된다면, \(\mu_X(B)=\lambda(B)\)
\(\forall B\in {\cal R}: \mu_X(B) \leq \lambda(B)\) 이므로 자명함
- 예제3 – 혼합된 균등분포
아래와 같은 distribution function \(F_X\)을 가지는 확률변수 \(X\)를 고려하자.
\[F_X(x) = \begin{cases} 0 & x<0\\ \frac{3}{2}x & 0\leq x < \frac{1}{2} \\ \frac{1}{2}+\frac{1}{2}x & \frac{1}{2}\leq x<1 \\ 1 & 1\leq x\end{cases}\]
이러한 함수 \(F_X\)는 르벡메져에 대하여 absolutely continuous 한가?
(해설)
\(\forall B \in {\cal R}: \mu_X(B) \leq \frac{3}{2}\lambda(B)\) 이므로 자명함.
예제2,3으로 관찰하고 착각할 수 있는 것: 그냥 연속이면 다 절대연속 아니야?
- 예제4 – 칸토어함수
칸토어함수 \(F_X\)는 르벡메져에 대하여 absolutely continuous 하지 않다.
\(f_X\)는 존재하지 않는당. 절대연속이 아니당
(해설)
(귀류법)
칸토어함수 \(F_X\)가 absolutely continuous 하다고 하자. 그러면 \(\mu_X((a,b]) = \mu_X([a,b])\) 가 성립한다.
RHS= \(\mu_X(\{a\})+\mu_X((a,b])=0+\mu_X((a,b])\)=LHS
\(\lambda(\{a\})=0 \rightarrow \mu_X(\{a\})=0 \because \mu_x << \lambda\)
\(n=0\):
- \(C_0=[0,1]\)
- \(\mu_X(C_0)=\mu_X((0,1])=F_X(1)-F_X(0)=1\)
\(n=1\):
- \(C_1=[0,\frac{1}{3}] \cup [\frac{2}{3},1]\)
- \(\mu_X(C_1)=\mu_X((0,\frac{1}{3}])+\mu_X((\frac{2}{3},1])=F_X(\frac{1}{3})-F_X(0)+F_X(1)-F_X(\frac{2}{3})=1\)
정리하면 아래와 같다.
| \(n\) | \(C_n\) | \(\mu_X(C_n)\) |
|---|---|---|
| \(0\) | \([0,1]\) | \(1\) |
| \(1\) | \([0,\frac{1}{3}] \cup [\frac{2}{3},1]\) | \(1\) |
| \(2\) | \([0,\frac{1}{9}]\cup[\frac{2}{9},\frac{1}{3}] \cup[\frac{2}{3},\frac{7}{9}]\cup [\frac{8}{9},1]\) | \(1\) |
| \(\dots\) | \(\dots\) | \(1\) |
그런데 \(\lambda({\cal C})=0\) 이지만 \(\mu_X(\lim_{n\to \infty}C_n)=\mu_X({\cal C})=1\) 이므로 \(\mu<<\lambda\)에 모순이다.
라돈니코딤 정리
- 이론: 분포함수 \(F_X:\mathbb{R} \to [0,1]\)가 (르벡메져에 대하여) 절대연속이라면 아래를 만족하는 함수 \(f_X:\mathbb{R} \to \mathbb{R}^+\)가 존재한다.
\[F_X = \int_{(-\infty,x]}f_Xd\lambda\]
여기에서 함수 \(f_X\)를 \(F_X\)의 밀도함수 (density function) 이라고 한다. 일반적으로 밀도함수 \(f_X\)는 유일하지 않지만, 르벡측도로 재었을때 0인 집합을 제외한 부분에서는 유일하게 결정된다. (요약: 분포함수 \(F_X\)가 절대연속이면 밀도함수 \(f_X\)가 존재하고, 거의 유일함)
위에서 “르벡측도로 재었을때 0인 집합을 제외한 부분에서는 유일하게 결정된다”라는 부분은 “르벡메져 \(\lambda\)에 대하여 거의 유일하다” 라고 이해해도 무방. 엄밀하게 쓰면 “분포함수 \(F_X\)가 있다면 밀도함수의 정의하는 만족하는 함수가 반드시 하나는 존재한다. 만약에 두 함수 \(f\)와 \(g\)가 모두 밀도함수의 정의를 만족한다면 ‘\(f=g\) a.e. with respect to \(\lambda\)’ 가 성립한다.” 와 같은 식으로 쓸 수 있음.
위에서 \(f\)의 공역이 \(\mathbb{R}^+\)인 이유는 \(F_X\)가 증가함수라서..
- Thm (라돈니코딤 정리)[@durrett2019probability, Thm A.4.8.]: 가측공간 \((S,{\cal S})\)를 고려하자. 그리고 \(\mu\)와 \(\lambda\)가 \((S,{\cal S})\)에서의 \(\sigma\)-finite measure 라고 하자. 만약에 \(\mu << \lambda\) 이라면 아래를 만족하는 가측함수 \(f:(S,{\cal S}) \to (\mathbb{R}^+,{\cal R^+})\)가 거의 유일하게 (w.r.t. \(\lambda\)) 존재한다.
\[\forall B \in {\cal S}:~ \mu(B) = \int_B f d\lambda.\]
여기에서 \(f\)를 Radon-Nikodym derivative of \(\mu\) w.r.t. \(\lambda\) 라고 하며, 이러한 의미에서 \(f=\frac{d\mu}{d\lambda}\)와 같이 표현하기도 한다.
\(\mu\)를 \(\lambda\)로 미분한거로 생각,, 실제 미분은 아니고 미분한거라 생각
- 예제1 – 균등분포
아래와 같은 함수를 고려하자.
\[F_X(x) = \begin{cases} 0 & x<0 \\ x & 0\leq x \leq 1 \\ 1 & x> 1 \\ \end{cases}\]
또한 아래와 같은 함수 \(f_X: \mathbb{R} \to \mathbb{R}\) 를 고려하자.
\[f_X(x) = \begin{cases} 1 & 0 \leq x \leq 1 \\ 0 & o.w. \end{cases}\]
\(f_X(x)\)가 \(F_X(x)\)의 라돈니코딤 도함수임을 설명하라.
(해설)
- \(\mu_X\)와 \(\lambda\)는 모두 \((\mathbb{R},{\cal R})\)에서 \(\sigma\)-finite 하다.
\(F_X(x)\)에 대응하는 \(\mu_X\)가 있다.
\(\sigma\)-finite msr는 \(\lambda({\cal R})=\infty\)인 것은 상관없지만 \(A_1,a_2,\dots \in {\cal R}\)이고 (1). \(\lambda(A_n) < \infty, \forall n \in \mathbb{N}\), (2). \(\cup_{n=1}^\infty A_n = \mathbb{R}\)
만약 \(A_n=(-n,n)\)으로 잡게 되면 \(\lambda(A_n)=2n<\infty, \forall n \in {\cal N}\)이고 증가하는 수열이므로 \(lim_{n \to \infty} A_n = \mathbb{R}\)이므로 \(\sigma\)-finte msr가 된다.ㅡ
- \(\mu_X << \lambda\)이다. 따라서 적당한 \({\cal R} \to {\cal R}\) measurable function이 존재하여 라돈니코딤 도함수의 조건을 만족함을 알 수 있다.
\(F_X\)가 절대연속이고, \(\forall B \in {\cal R}: \mu_X(B) \leq \lambda(B)\)
\(\forall B \in {\cal R}:~ \mu(B) = \int_B f d\lambda.\) 를보이면 된다.
\(B=(-\infty, x]\)라고 놓으면 \(\mu(B)=F_X(x)=\int_B f d\lambda\)
\(B \in {\cal R}\)인 경우에 위와같은 증명을 보이려면… 밑 6번에 교수님 풀이 참고 ㅎ
- 우리가 생각하는 후보는 \(f_X\)인데 이것이 만약에 (1) \({\cal R} \to {\cal R}\) 가측함수이고 (2) 라돈니코딤 도함수의 조건을 만족한다면 \(f_X\)는 \(F_X\)의 거의 유일한 (w.r.t. \(\lambda\)) 밀도함수라고 주장할 수 있다.
- \(f_X\)는 simple function이므로 \({\cal R} \to {\cal R}\) 가측함수이다.
- 임의의 \(x\)에 대하여 \(F_X(x)=\mu_X((-\infty,x])=\int_{(-\infty,x]}f_Xd\lambda\) 이 성립한다.
- 5와 \(\pi\)-\(\lambda\) thm을 이용하면 모든 \(B \in {\cal R}\)에 대하여 \(\mu_X(B) = \int_B f_X d\lambda\) 가 성립한다. (풀이참고)
- 따라서 \(f_X\)는 \(F_X\)의 밀도함수이다.
- 예제2 – 베르누이 분포
아래와 같은 함수를 고려하자.
\[F_X(x) = \begin{cases} 0 & x<0 \\ \frac{1}{2} & 0 \leq x <1 \\ 1 & x \geq 1 \end{cases}\]
이 함수에 대응하는 \(\mu_X\)를 아래와 같이 정의하자.
- \(\mu_X(\emptyset)=0\)
- \(\mu_X(\{0\})=\frac{1}{2}\)
- \(\mu_X(\{1\})=\frac{1}{2}\)
- \(\mu_X(\{0,1\})=1\)
- \(\mu_X(B)=0\) , \(B \in {\cal R} - \{0,1\} - \{0\} - \{1\}\)
\(\mu_X\)는 \(\lambda\)에 대한 라돈니코딤 도함수를 가지지 않음을 보여라.
(해설) – 절대연속이 안되는걸?
\(\mu_X << \lambda\)가 성립하지 않는다. \((\mathbb{R},{\cal R})\)에서!