해당 강의노트는 전북대학교 이영미교수님 2022-2 고급회귀분석론 자료임

import

library(ggplot2)

데이터

############ 데이터 불러오기 
dt <- data.frame(x = c(4,8,9,8,8,12,6,10,6,9),
                 y = c(9,20,22,15,17,30,18,25,10,20))
dt

A data.frame: 10 × 2
x	y
<dbl>	<dbl>
4	9
8	20
9	22
8	15
8	17
12	30
6	18
10	25
6	10
9	20

cor(dt$x, dt$y)

0.921812343945765

plot(y~x, 
     data = dt,
     xlab = "광고료",
     ylab = "총판매액",
     pch  = 16,
     cex  = 2,
     col  = "darkorange")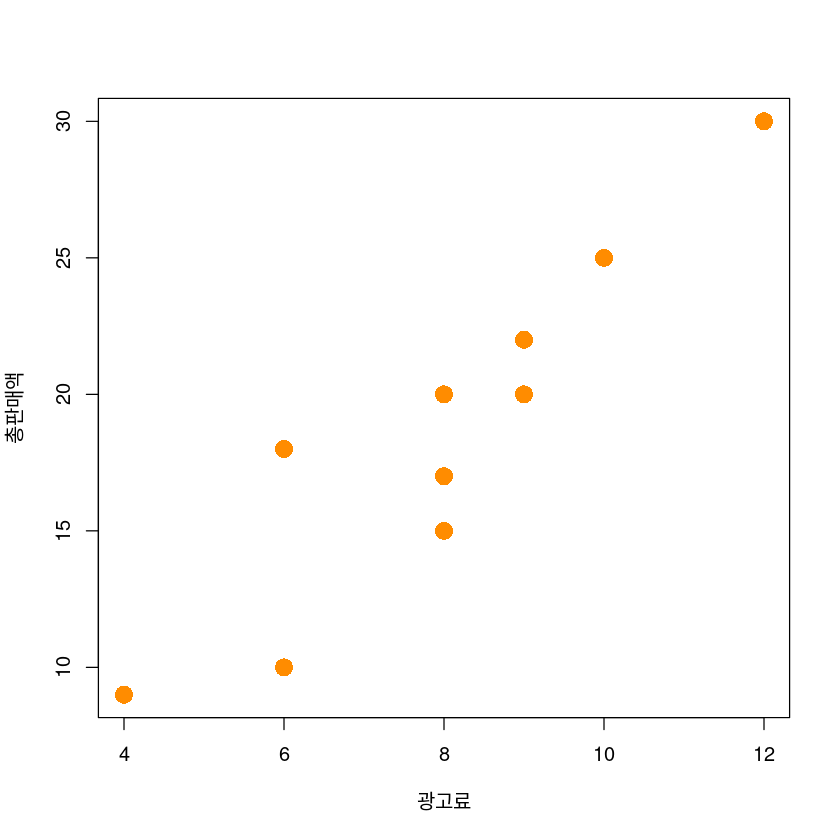

ggplot(dt, aes(x, y)) +
  geom_point(col='steelblue', lwd=2) +
  # geom_abline(intercept = co[1], slope = co[2], col='darkorange', lwd=1.2) +
  xlab("광고료")+ylab("총판매액")+
  # scale_x_continuous(breaks = seq(1,10))+
  theme_bw() +
  theme(axis.title = element_text(size = 14))

Warning message in geom_point(col = "steelblue", lwd = 2):
“Ignoring unknown parameters: `linewidth`”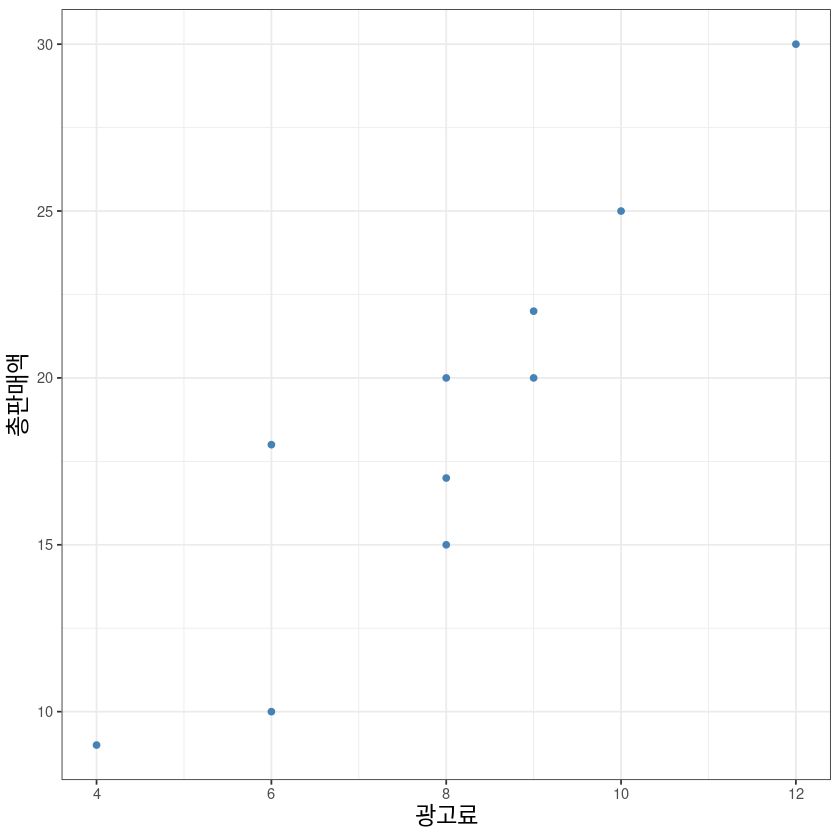

적합

hat y = hat (E(y|X=x)) = hat beta_0 +hat beta_1 * x
H0 : beta0 =0 vs H1 : beta0 != 0
H0 : beta1 =0 vs H1 : beta1 != 0

## y = beta0 + beta1*x + epsilon
model1 <- lm(y ~ x, dt)
model1


Call:
lm(formula = y ~ x, data = dt)

Coefficients:
(Intercept)            x  
     -2.270        2.609

summary(model1)


Call:
lm(formula = y ~ x, data = dt)

Residuals:
   Min     1Q Median     3Q    Max 
-3.600 -1.502  0.813  1.128  4.617 

Coefficients:
            Estimate Std. Error t value Pr(>|t|)    
(Intercept)  -2.2696     3.2123  -0.707 0.499926    
x             2.6087     0.3878   6.726 0.000149 ***
---
Signif. codes:  0 ‘***’ 0.001 ‘**’ 0.01 ‘*’ 0.05 ‘.’ 0.1 ‘ ’ 1

Residual standard error: 2.631 on 8 degrees of freedom
Multiple R-squared:  0.8497,    Adjusted R-squared:  0.831 
F-statistic: 45.24 on 1 and 8 DF,  p-value: 0.0001487

names(model1)

'coefficients'
'residuals'
'effects'
'rank'
'fitted.values'
'assign'
'qr'
'df.residual'
'xlevels'
'call'
'terms'
'model'

model1$fitted.values  ##hat y
model1$coefficients

1: 8.16521739130434
2: 18.6
3: 21.2086956521739
4: 18.6
5: 18.6
6: 29.0347826086957
7: 13.3826086956522
8: 23.8173913043478
9: 13.3826086956522
10: 21.2086956521739

(Intercept): -2.2695652173913
x: 2.60869565217391

anova(model1)  ## 회귀모형의 유의성 검정

A anova: 2 × 5
	Df	Sum Sq	Mean Sq	F value	Pr(>F)
	<int>	<dbl>	<dbl>	<dbl>	<dbl>
x	1	313.04348	313.043478	45.24034	0.0001486582
Residuals	8	55.35652	6.919565	NA	NA

a <- summary(model1)
ls(a)

'adj.r.squared'
'aliased'
'call'
'coefficients'
'cov.unscaled'
'df'
'fstatistic'
'r.squared'
'residuals'
'sigma'
'terms'

summary(model1)$coef   ## 회귀계수의 유의성 검정

A matrix: 2 × 4 of type dbl
	Estimate	Std. Error	t value	Pr(>\|t\|)
(Intercept)	-2.269565	3.212348	-0.7065129	0.4999255886
x	2.608696	0.387847	6.7260939	0.0001486582

confint(model1, level = 0.95)  ##회귀계수의 신뢰구간

A matrix: 2 × 2 of type dbl
	2.5 %	97.5 %
(Intercept)	-9.677252	5.138122
x	1.714319	3.503073

## beta +- t_alpha/2 (n-2) * se(beta)
qt(0.025, 8)
qt(0.975, 8)

-2.30600413520417

2.30600413520417

## y = beta1*x + epsilon
model2 <- lm(y ~ 0 + x, dt)
summary(model2)


Call:
lm(formula = y ~ 0 + x, data = dt)

Residuals:
    Min      1Q  Median      3Q     Max 
-4.0641 -1.5882  0.2638  1.4818  3.9359 

Coefficients:
  Estimate Std. Error t value Pr(>|t|)    
x   2.3440     0.0976   24.02  1.8e-09 ***
---
Signif. codes:  0 ‘***’ 0.001 ‘**’ 0.01 ‘*’ 0.05 ‘.’ 0.1 ‘ ’ 1

Residual standard error: 2.556 on 9 degrees of freedom
Multiple R-squared:  0.9846,    Adjusted R-squared:  0.9829 
F-statistic: 576.8 on 1 and 9 DF,  p-value: 1.798e-09

plot(y~x, data = dt,
     xlab = "광고료",
     ylab = "총판매액",
     pch  = 20,
     cex  = 2,
     col  = "darkorange")
abline(model1, col='steelblue', lwd=2)
abline(model2, col='green', lwd=2)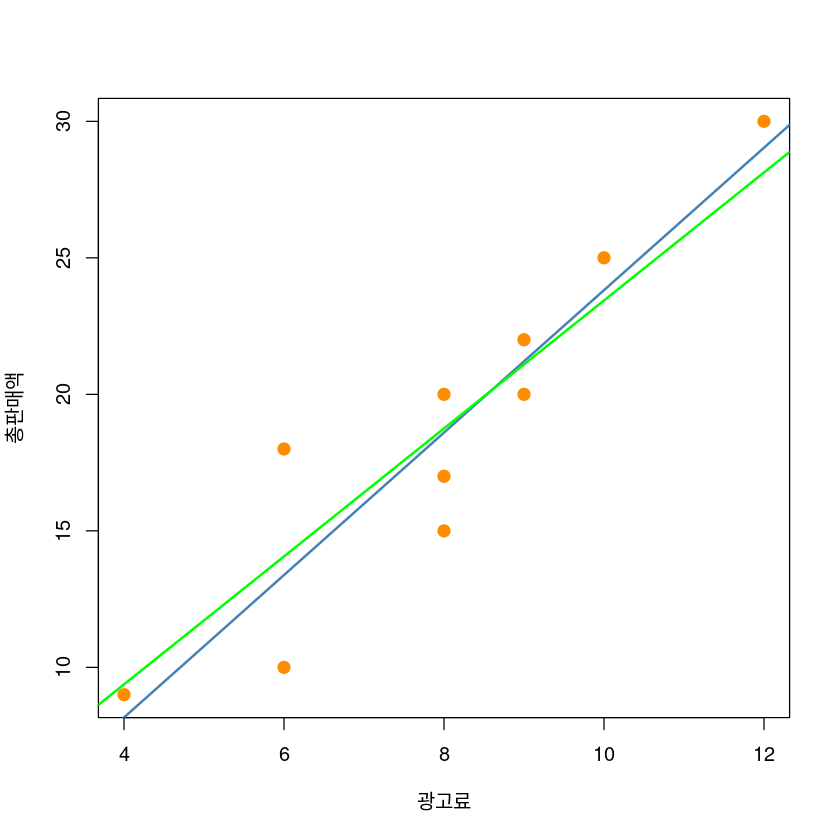

co <- coef(model1)

ggplot(dt, aes(x, y)) +
  geom_point(col='steelblue', lwd=1) +
  geom_abline(intercept = co[1], slope = co[2], col='darkorange', lwd=1) +
  xlab("광고료")+ylab("총판매액")+
  theme_bw()+
  theme(axis.title = element_text(size = 16))

Warning message in geom_point(col = "steelblue", lwd = 1):
“Ignoring unknown parameters: `linewidth`”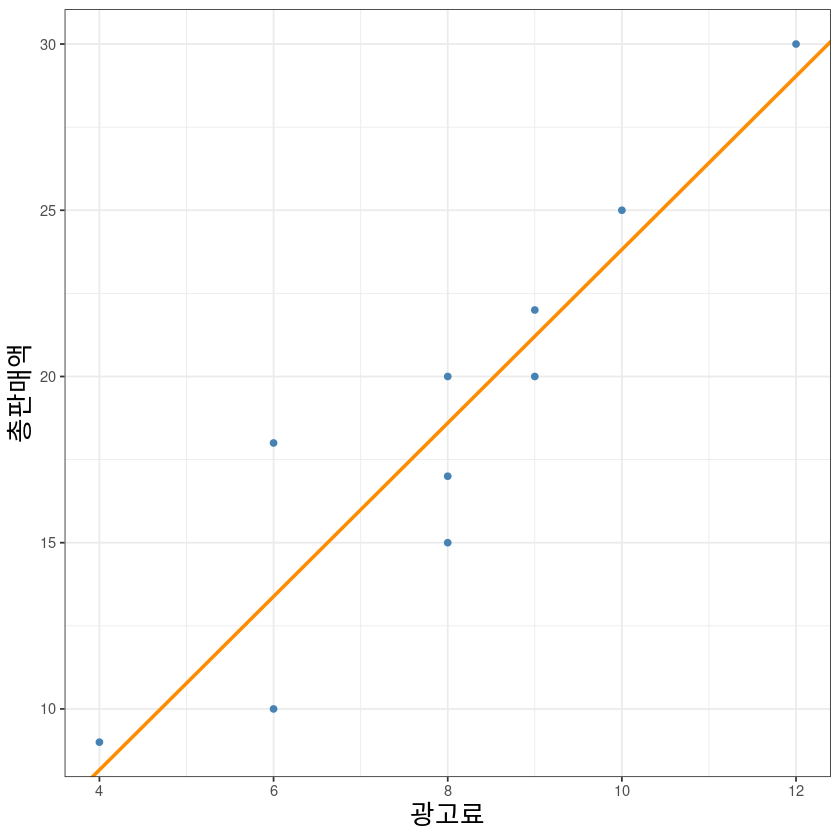

LSE 구하기

dt1 <- data.frame(
  i = 1:nrow(dt),
  x = dt$x,
  y = dt$y,
  x_barx = dt$x - mean(dt$x),
  y_bary = dt$y - mean(dt$y))

dt1$x_barx2 <- dt1$x_barx^2
dt1$y_bary2 <- dt1$y_bary^2
dt1$xy <-dt1$x_barx * dt1$y_bary

dt1

A data.frame: 10 × 8
i	x	y	x_barx	y_bary	x_barx2	y_bary2	xy
<int>	<dbl>	<dbl>	<dbl>	<dbl>	<dbl>	<dbl>	<dbl>
1	4	9	-4	-9.6	16	92.16	38.4
2	8	20	0	1.4	0	1.96	0.0
3	9	22	1	3.4	1	11.56	3.4
4	8	15	0	-3.6	0	12.96	0.0
5	8	17	0	-1.6	0	2.56	0.0
6	12	30	4	11.4	16	129.96	45.6
7	6	18	-2	-0.6	4	0.36	1.2
8	10	25	2	6.4	4	40.96	12.8
9	6	10	-2	-8.6	4	73.96	17.2
10	9	20	1	1.4	1	1.96	1.4

round(colSums(dt1),3)

i: 55
x: 80
y: 186
x_barx: 0
y_bary: 0
x_barx2: 46
y_bary2: 368.4
xy: 120

### hat beta1 = S_xy / S_xx
##hat beta0 = bar y - hat beta_1 * bar x
beta1 <- as.numeric(colSums(dt1)[8]/colSums(dt1)[6])
beta0 <- mean(dt$y) - beta1 *  mean(dt$x)

cat("hat beta0 = ", beta0)

hat beta0 =  -2.269565

cat("hat beta1 = ", beta1)

hat beta1 =  2.608696

평균반응, 개별 y 추정

############
## E(Y|x0), y = E(Y|x0) + epsilon
# x0 = 4.5
new_dt <- data.frame(x = 4.5)

# hat y0 = hat beta0 + hat beta1 * 4.5

predict(model1, 
        newdata = new_dt,
        interval = c("confidence"), level = 0.95)

A matrix: 1 × 3 of type dbl
	fit	lwr	upr
1	9.469565	5.79826	13.14087

predict(model1, newdata = new_dt, 
        interval = c("prediction"), level = 0.95)

A matrix: 1 × 3 of type dbl
	fit	lwr	upr
1	9.469565	2.379125	16.56001

dt_pred <- data.frame(
  x = 1:12,
  predict(model1, 
          newdata=data.frame(x=1:12), 
          interval="confidence", level = 0.95))
dt_pred

A data.frame: 12 × 4
	x	fit	lwr	upr
	<int>	<dbl>	<dbl>	<dbl>
1	1	0.3391304	-6.2087835	6.887044
2	2	2.9478261	-2.7509762	8.646628
3	3	5.5565217	0.6905854	10.422458
4	4	8.1652174	4.1058891	12.224546
5	5	10.7739130	7.4756140	14.072212
6	6	13.3826087	10.7597808	16.005437
7	7	15.9913043	13.8748223	18.107786
8	8	18.6000000	16.6817753	20.518225
9	9	21.2086957	19.0922136	23.325178
10	10	23.8173913	21.1945634	26.440219
11	11	26.4260870	23.1277880	29.724386
12	12	29.0347826	24.9754543	33.094111

dt_pred2 <- as.data.frame(predict(model1, 
                                  newdata=data.frame(x=1:12), 
                                  interval="prediction", level = 0.95))
dt_pred2

A data.frame: 12 × 3
	fit	lwr	upr
	<dbl>	<dbl>	<dbl>
1	0.3391304	-8.5867330	9.264994
2	2.9478261	-5.3751666	11.270819
3	5.5565217	-2.2199297	13.332973
4	8.1652174	0.8663128	15.464122
5	10.7739130	3.8692308	17.678595
6	13.3826087	6.7738957	19.991322
7	15.9913043	9.5667143	22.415894
8	18.6000000	12.2379683	24.962032
9	21.2086957	14.7841056	27.633286
10	23.8173913	17.2086783	30.426104
11	26.4260870	19.5214047	33.330769
12	29.0347826	21.7358781	36.333687

names(dt_pred2)[2:3] <- c('plwr', 'pupr')

dt_pred3 <- cbind.data.frame(dt_pred, dt_pred2[,2:3])

barx <- mean(dt$x)
bary <- mean(dt$y)

plot(y~x, data = dt,
     xlab = "광고료",
     ylab = "총판매액",
     pch  = 20,
     cex  = 2,
     col  = "grey",
     ylim = c(min(dt_pred3$plwr), max(dt_pred3$pupr)))
abline(model1, lwd = 5, col = "darkorange")
lines(dt_pred3$x, dt_pred3$lwr, col = "dodgerblue", lwd = 3, lty = 2)
lines(dt_pred3$x, dt_pred3$upr, col = "dodgerblue", lwd = 3, lty = 2)
lines(dt_pred3$x, dt_pred3$plwr, col = "dodgerblue", lwd = 3, lty = 3)
lines(dt_pred3$x, dt_pred3$pupr, col = "dodgerblue", lwd = 3, lty = 3)
abline(h=bary,v=barx, lty=2, lwd=0.2, col='dark grey')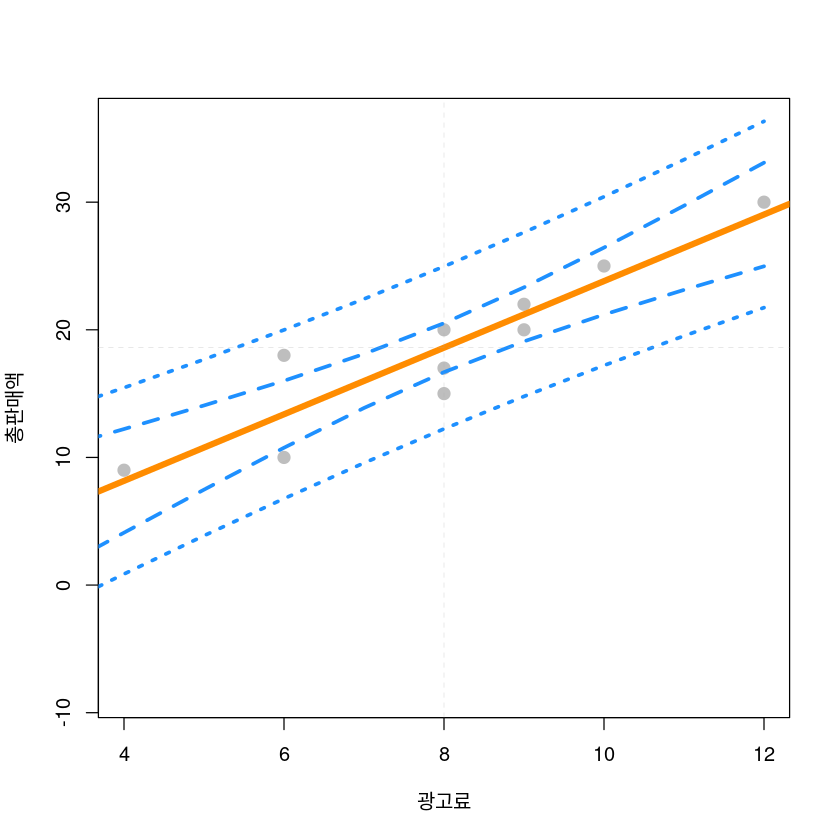

ggplot(dt_pred3, aes(x, fit)) +
  geom_line(col='steelblue', lwd=2) +
  xlab("")+ylab("")+
  scale_x_continuous(breaks = seq(1,10))+
  geom_line(aes(x, lwr), lty=2, lwd=1.5, col='darkorange') +
  geom_line(aes(x, upr), lty=2, lwd=1.5, col='darkorange') +
  geom_line(aes(x, plwr), lty=2, lwd=1.5, col='dodgerblue') +
  geom_line(aes(x, pupr), lty=2, lwd=1.5, col='dodgerblue') +
  geom_vline(xintercept = barx, lty=2, lwd=0.2, col='dark grey')+
  geom_hline(yintercept = bary, lty=2, lwd=0.2, col='dark grey')+
  theme_bw()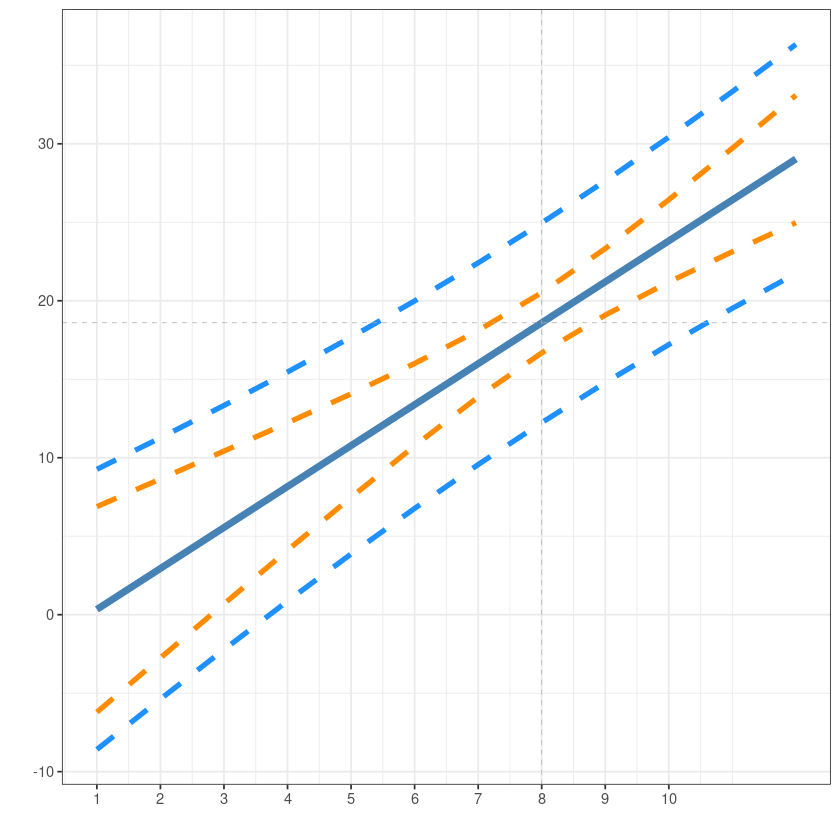

bb <- summary(model1)$sigma * ( 1 + 1/10 +(dt$x - 8)^2/46)
dt$ma95y <- model1$fitted + 2.306*bb
dt$mi95y <- model1$fitted - 2.306*bb

ggplot(dt, aes(x=x, y=y)) +
  geom_point() +
  geom_smooth(method=lm , color="red", fill="#69b3a2", se=TRUE) +
  geom_line(aes(x, mi95y), col = 'darkgrey', lty=2) +
  geom_line(aes(x, ma95y), col = 'darkgrey', lty=2) +
  theme_bw() +
  theme(axis.title = element_blank())

`geom_smooth()` using formula = 'y ~ x'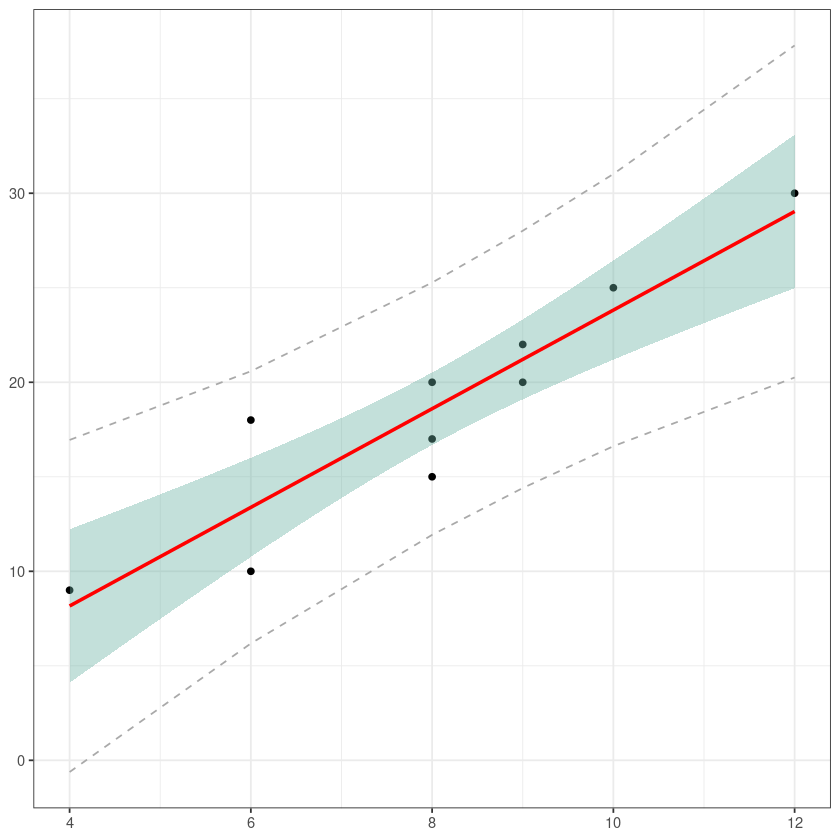

잔차분석

epsilon : 선형성, 등분산성, 정규성, 독립성

dt

A data.frame: 10 × 4
x	y	ma95y	mi95y
<dbl>	<dbl>	<dbl>	<dbl>
4	9	16.94766	-0.6172208
8	20	25.27254	11.9274568
9	22	28.01311	14.4042841
8	15	25.27254	11.9274568
8	17	25.27254	11.9274568
12	30	37.81722	20.2523444
6	18	20.58263	6.1825918
10	25	31.01741	16.6173744
6	10	20.58263	6.1825918
9	20	28.01311	14.4042841

dt$yhat <- model1$fitted

# fitted.values(model1)
dt$resid <- model1$residuals


# resid(model1)

par(mfrow=c(1,2))
plot(resid ~ x, dt, pch=16, ylab = 'Residual')
abline(h=0, lty=2, col='grey')
plot(resid ~ yhat, dt, pch=16, ylab = 'Residual')
abline(h=0, lty=2, col='grey')
par(mfrow=c(1,1))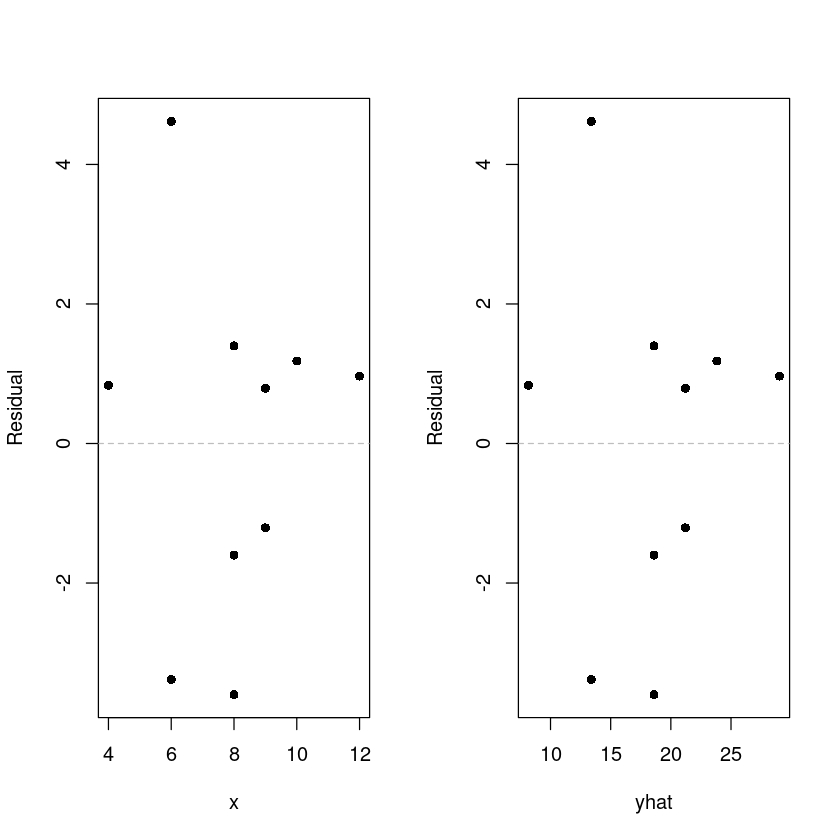


# 독립성검정 : DW test
library(lmtest)
## 
dwtest(model1, alternative = "two.sided")  #H0 : uncorrelated vs H1 : rho != 0
# dwtest(model1, alternative = "greater")  #H0 : uncorrelated vs H1 : rho > 0
# dwtest(model1, alternative = "less")

Loading required package: zoo


Attaching package: ‘zoo’


The following objects are masked from ‘package:base’:

    as.Date, as.Date.numeric


    Durbin-Watson test

data:  model1
DW = 1.4679, p-value = 0.3916
alternative hypothesis: true autocorrelation is not 0

## 정규분포 (QQ plot)
qqnorm(dt$resid, pch=16)
qqline(dt$resid, col = 2)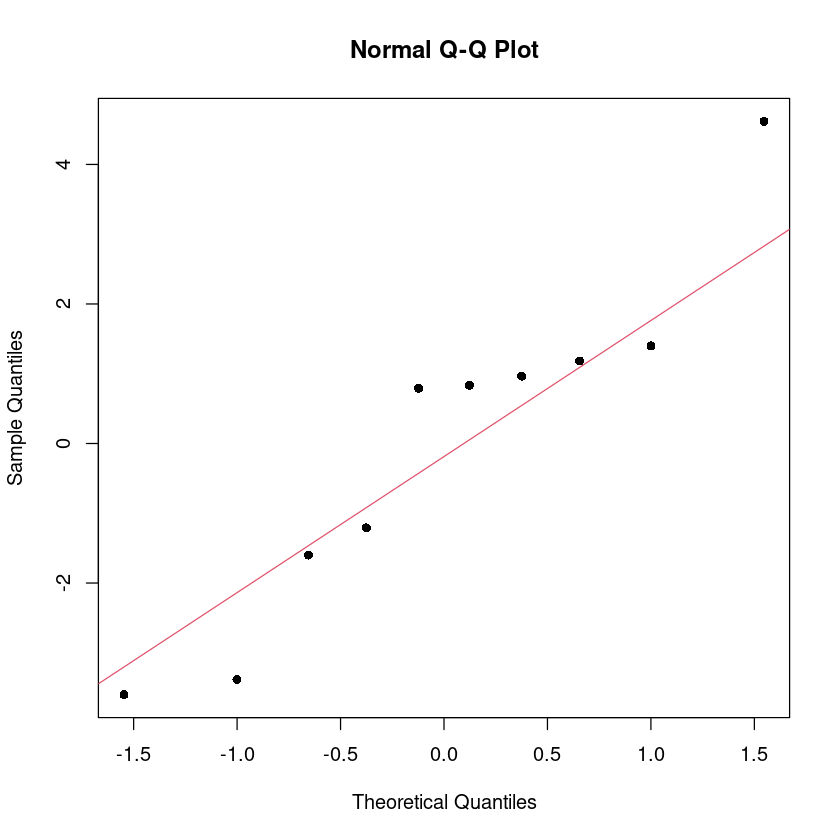

ggplot(dt, aes(sample = resid)) + 
  stat_qq() + stat_qq_line() +
  theme_bw()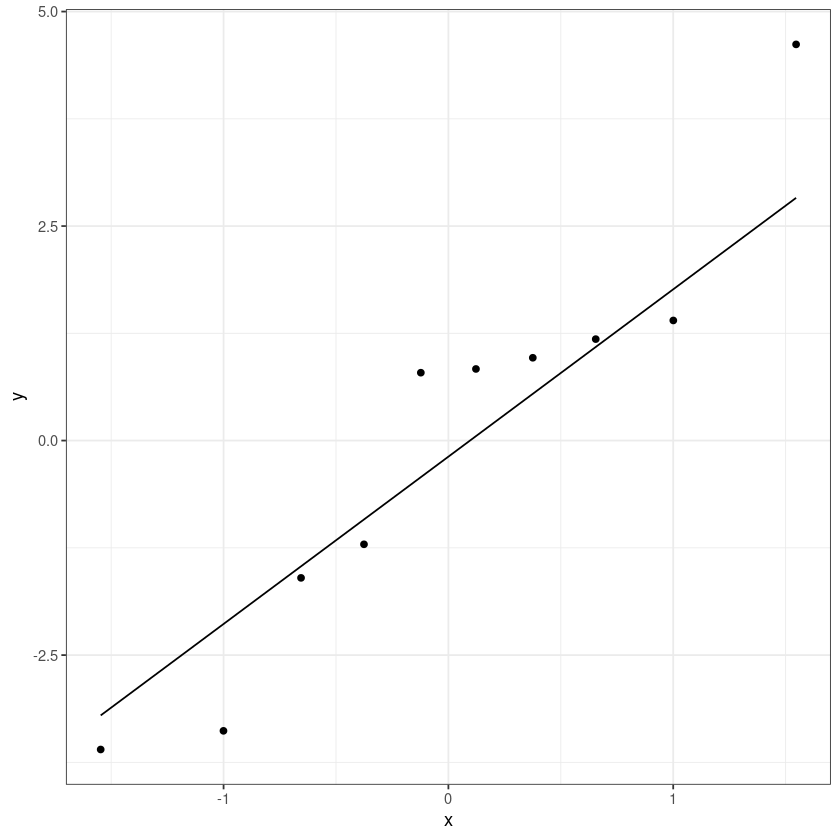

## 정규분포 검정 
shapiro.test(dt$resid)  ##shapiro-wilk test
#H0 : normal distributed vs H1 : not


    Shapiro-Wilk normality test

data:  dt$resid
W = 0.92426, p-value = 0.3939

## 등분산성 검정 
bptest(model1) #Breusch–Pagan test
# H0 : 등분산 vs H1 : 이분산


    studentized Breusch-Pagan test

data:  model1
BP = 1.6727, df = 1, p-value = 0.1959

install.packages('UsingR')
library(UsingR)
data(father.son)

Installing package into ‘/home/coco/R/x86_64-pc-linux-gnu-library/4.2’
(as ‘lib’ is unspecified)

also installing the dependency ‘HistData’


Loading required package: MASS

Loading required package: HistData

Loading required package: Hmisc

Loading required package: lattice

Loading required package: survival

Loading required package: Formula


Attaching package: ‘Hmisc’


The following objects are masked from ‘package:base’:

    format.pval, units



Attaching package: ‘UsingR’


The following object is masked from ‘package:survival’:

    cancer

names(father.son)

'fheight'
'sheight'

lm.fit<-lm(sheight~fheight, data=father.son)
summary(lm.fit)


Call:
lm(formula = sheight ~ fheight, data = father.son)

Residuals:
    Min      1Q  Median      3Q     Max 
-8.8772 -1.5144 -0.0079  1.6285  8.9685 

Coefficients:
            Estimate Std. Error t value Pr(>|t|)    
(Intercept) 33.88660    1.83235   18.49   <2e-16 ***
fheight      0.51409    0.02705   19.01   <2e-16 ***
---
Signif. codes:  0 ‘***’ 0.001 ‘**’ 0.01 ‘*’ 0.05 ‘.’ 0.1 ‘ ’ 1

Residual standard error: 2.437 on 1076 degrees of freedom
Multiple R-squared:  0.2513,    Adjusted R-squared:  0.2506 
F-statistic: 361.2 on 1 and 1076 DF,  p-value: < 2.2e-16

plot(sheight~fheight, 
     data=father.son, 
     pch=16, cex=0.5,
     xlab="father’s height (inches)", 
     ylab="son’s height (inches)")
abline(lm.fit)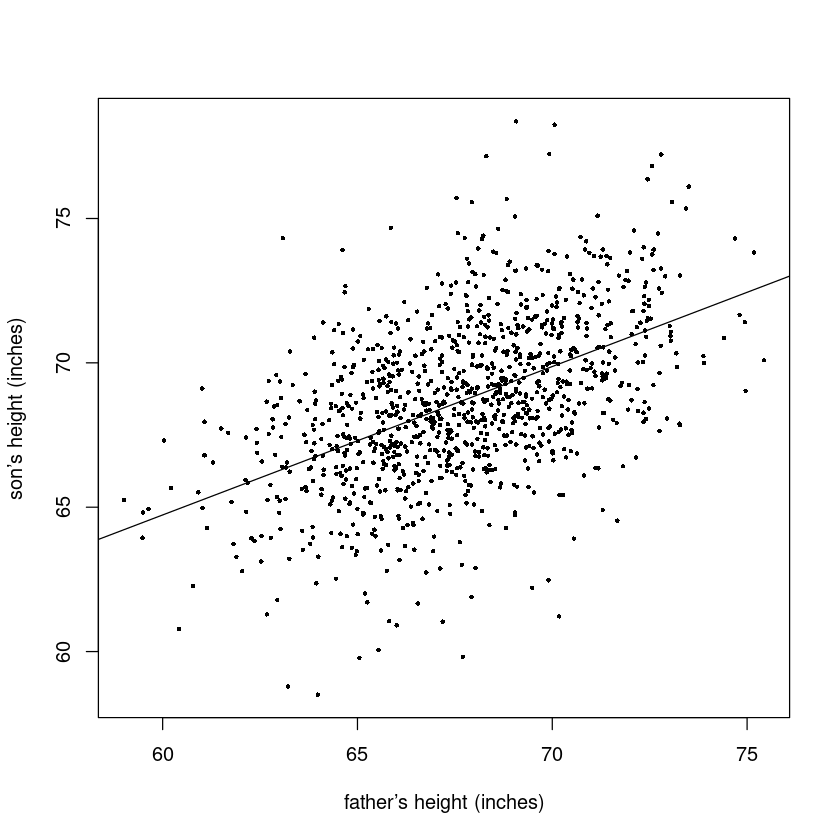

amazon<-read.csv("amazon.csv")
plot(High   ~Year  , amazon, pch=16)
lm.fit<-lm(High~Year, data=amazon)
summary(lm.fit)

confint(lm.fit)

par(mfrow=c(1,2))
scatter.smooth(x=1:length(amazon$Year), y=residuals(lm.fit), xlab="Year")
scatter.smooth(x=predict(lm.fit), y=residuals(lm.fit), xlab=expression(hat(y)))

library(lmtest)
dwtest(lm.fit)