1번. 다음을 증명하시오.
(1)
\(Z\) ~ \(N(0,1)\)이면 \(Z^2\) ~ \(\chi_1^2\)이다.
\(Y=Z^2\)
\(F_Y(y) = P(Y \leq y) = P(Z^2 \leq y)=P(-\sqrt{y} \leq Z \leq \sqrt{y})=\Phi(\sqrt{y})-\Phi(-\sqrt{y})\)
\(f_Y(y) = \dfrac{d}{dy}F_Y(y) = \Phi(\sqrt{y})\dfrac{1}{2\sqrt{y}}-\Phi(-\sqrt{y}) \left(-\dfrac{1}{2\sqrt{y}} \right)=\dfrac{1}{\sqrt{2\pi}}e^{-2/y} \dfrac{1}{\sqrt{y}}=\dfrac{1}{\Gamma{(1/2)}2^{1/2}}y^{-1/2}e^{-2/y}\)
즉, \(r=1\)인 카이제곱 분포를 따른다.
(2)
랜덤표본 \(X_1, \dots, X_n\)에 대하여 \(Cov(\bar X_n, X_k - \bar X_n)=0\)
\(Cov(\bar X, X_k-\bar X) = Cov(\bar X, X_k) - Cov(\bar X, \bar X) = Cov(\bar X, X_k) - Var(\bar X)\)
\(Cov(\bar X, X_k) = Cov(\frac{1}{n}X_1+\dots+\frac{1}{n}X_n, X_k)=\frac{1}{n}Cov(X_1,X_k)+\dots+\frac{1}{n}Cov(X_n,X_k)=\frac{1}{n}Cov(X_k,X_k)=\frac{1}{n}Var(X_k)=\frac{1}{n} \sigma^2\)
\(\because Cov(X_i, X_k)\) 는 서로 독립이므로 \(Cov(X_i, X_k)=0\) (단 \(i \neq k\))
\(\therefore Cov(\bar X, X_k-\bar X)= Cov(\bar X, X_k) - Var(\bar X) = \frac{1}{n} \sigma^2 - \frac{1}{n} \sigma^2 = 0\)
2번
\(GAM(\alpha, \beta)\)분포로부터의 랜덤표본 \(X_1, \dots, X_n\)에 대하여 \(\bar X_n\)의 분포를 구하시오.
\(\bar X_n = \sum_{i=1}^n X_i/n\)
\(E(\bar X_n)=\dfrac{1}{n} n \alpha \beta=\alpha \beta\), \(Var(\bar X_n)=\dfrac{1}{n^2} n\alpha \beta^2=\dfrac{1}{n} \alpha \beta^2\)
\(\bar X_n\) ~ \(GAM\left( \alpha \beta, \dfrac{1}{n} \alpha \beta^2 \right)\)
3번
\(N(\mu, \sigma^2)\)분포로부터의 랜덤표본 Suppose that \(X_1, \dots, X_n\)에 대하여 \(\sum_{i=1}^n(X_i-\bar X_n)^2/n\)의 분산을 구하시오
\(S_n^2 = \dfrac{\sum_{i=1}^n (X_i-\bar X_n)^2}{(n-1)}\)
\(\dfrac{(n-1)S_n^2}{\sigma^2} = \dfrac{\sum_{i=1}^n(X_i-\bar X)^2}{\sigma^2}\) ~ \(\chi_{n-1}^2\)
\(Var \left( \dfrac{\sum_{i=1}^n(X_i-\bar X)^2}{n} \right) = Var \left( \dfrac{\sum_{i=1}^n(X_i-\bar X)^2}{\sigma^2} \dfrac{\sigma^2}{n} \right) = \dfrac{\sigma^4}{n^2} Var \left( \dfrac{\sum_{i=1}^n(X_i-\bar X)^2}{\sigma^2} \right)=\dfrac{2\sigma^4(n-1)}{n^2}\)
4번
\(X_1,\dots,X_{16}\)과 \(Y_1,\dots,Y_{25}\)은 각각 \(N(0,9)\)와 \(N(2,16)\)로부터의 서로 독립인 랜덤표본이라고 할 때
(1)
\(\bar X_{16} - \bar Y_{25}\)의 분포를 구하시오.
\(E(\bar X_{16} - \bar Y_{25}) = E(\bar X_{16}) - E(\bar Y_{25}) = 0-2 = -2\)
\(Var(\bar X_{16} - \bar Y_{25}) = Var(\bar X_{16})+Var( \bar Y_{25}) = \dfrac{9}{16}+\dfrac{16}{25}=\dfrac{481}{400}\)
\(\bar X_{16} - \bar Y_{25}\) ~ \(N(-2,\dfrac{481}{400})\)
(2)
\(\dfrac{24\sum_{i=1}^{16} X_i^2}{9 \sum_{i=1}^{25}(Y_i-\bar Y)^2}\)
\(U=\left( \sum_{i=1}^{16}\dfrac{X_i-0}{3} \right)^2\) ~ \(\chi_{16}^2\)
\(S_{25}^2=\dfrac{\sum_{i=1}^{25}(Y_i-\bar Y)^2}{24}\)
\(V=\dfrac{24S_{25}^2}{16}\) ~ \(\chi_{24}^2\)
\(\sum_{i=1}^{25}(Y_i-\bar Y)^2 = 24 S_{25}^2\)
\(\dfrac{24\sum_{i=1}^{16} X_i^2}{9 \sum_{i=1}^{25}(Y_i-\bar Y)^2}=\dfrac{24}{9} \dfrac{16 \times 9}{16 \times 24} \dfrac{U/16}{V/24}=F\)~\(F_{16,24}\)
5번
\(X_1,X_2,\dots\)은 평균이 \(\mu\)이고 분산이 \(\sigma^2\)인 동일한 분포를 따르고 독립이다.
\[\sqrt{n} \left( \frac{1}{\bar {X_n}} - \frac{1}{\mu} \right)\begin{aligned} d\\ \rightarrow \end{aligned}\]
-중심 극한 정리\(\bar {X_n}\) ~ \(N(\mu, \dfrac{\sigma^2}{n})\)
\(\dfrac{\bar{X_n}-\mu}{\sigma / \sqrt{n}}\) ~ \(N(0,1)\)
-델타 방법확률변수의 열 \(X_1,X_2,\dots\) 에 대해서
\(\sqrt{n}(X_n-\theta) \rightarrow^d N(0,\sigma^2)\)이라고 하자.
이 때, 함수 \(g(\theta)\)의 연속인 도함수 \(g'(\theta)\)가 존재하고 0이 아니면
\(\sqrt{n}(g(X_n) - g(\theta)) \rightarrow^d N(0,\sigma^2[g'(\theta)]^2)\)이 성립한다.
중심극한정리에 의해 표본크기 \(n\)이 커짐에 따라 \(\sqrt{n}(\bar X_n - \mu) \rightarrow^d N(0,\mu)\)가 성립한다.
\(g(x)=\dfrac{1}{x}\)를 고려하면, \(g'(x)=-\dfrac{1}{x^2}, g(\mu)=\dfrac{1}{\mu}, [g'(\mu)]^2=\dfrac{1}{\mu^4}\)이 된다.
따라서, \(\sqrt{n} \left( \frac{1}{\bar {X_n}} - \frac{1}{\mu} \right)\begin{aligned} d\\ \rightarrow \end{aligned} N(0, \dfrac{\sigma^2}{\mu^4})\)
6번
\(X_1, X_2,\dots, X_n\)이 다음 분포로부터의 랜덤표본일 때 해당 모수의 적률추정량과 최대가능도 추정량을 구하시오.
(1)
\(GAM(2,\theta)\)
\(\mu_1 = E(X) = 2\theta = \bar{X_n} \rightarrow \theta^{MME} = \dfrac{\bar X_n}{2}\)
\(\mu_1 = \bar X^1\)

(2)
\(f(x|\mu, \sigma) = \dfrac{1}{\sigma} e^{-\frac{x-\mu}{\sigma}}I(x>\mu)\)
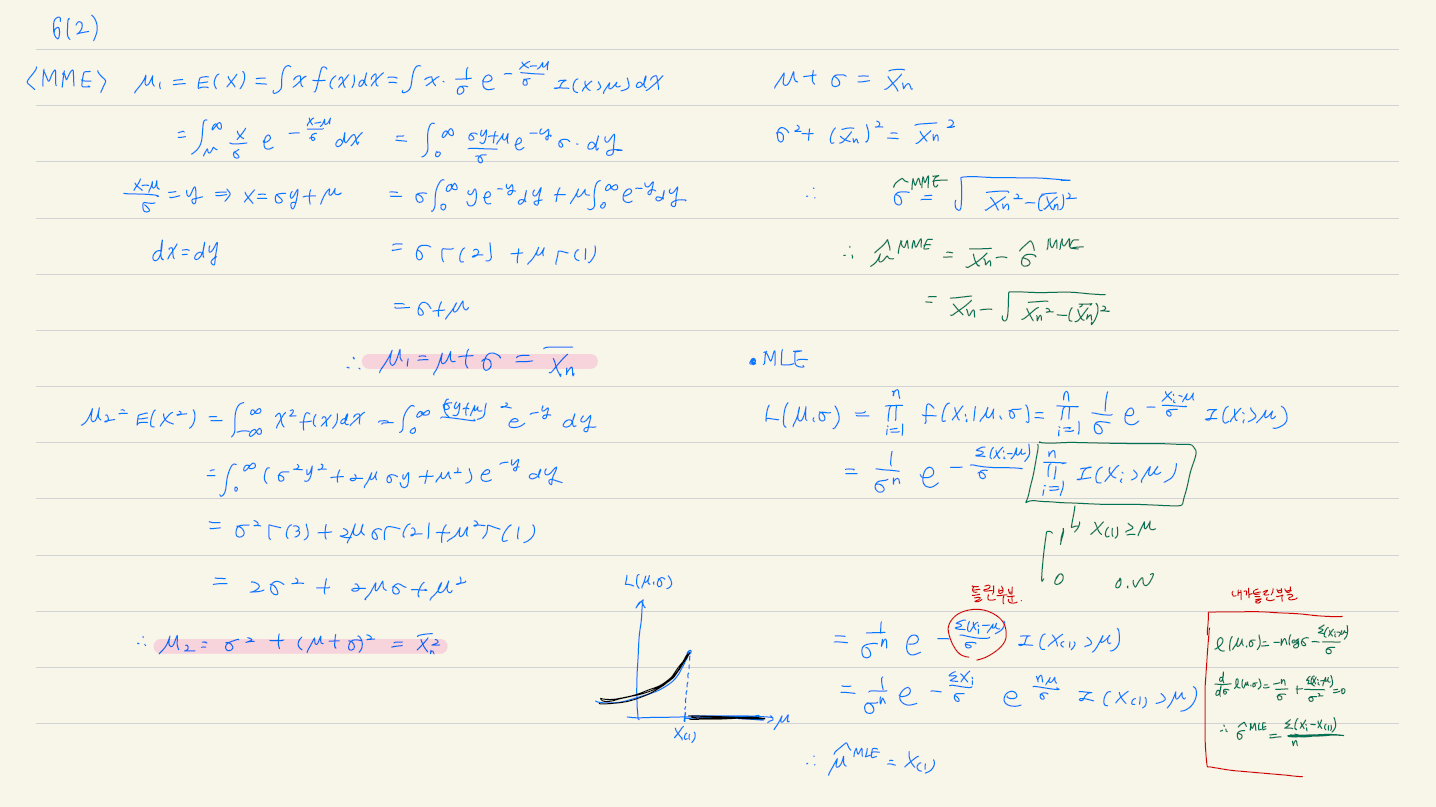
(3)
\(f(x|\theta) = \dfrac{3\theta^3}{x^4}I(\theta<x)\)
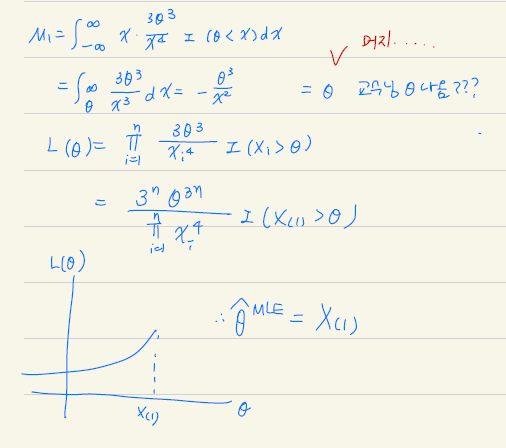
7번
\(X_1, X_2, \dots , X_n\)이 \(U(µ − 3 \sqrt{\sigma}, µ + 3 \sqrt{\sigma})\)로부터의 랜덤표본일 때 \(µ\)와 \(σ\)의 적률추정량을 구하시오
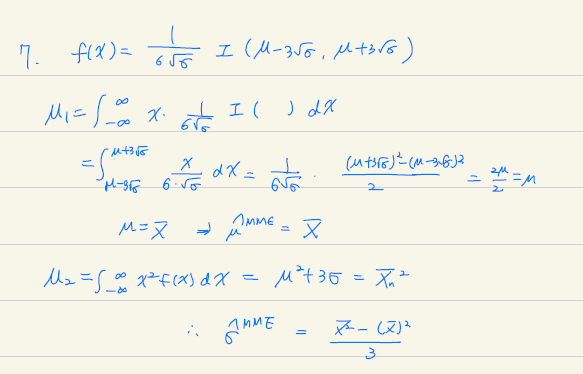
8번
\(X_1, X_2, \dots, X_n\)이 \(POI(λ)\)로부터의 랜덤표본일 때 \(g(λ) = 1/λ\) 의 최대가능도 추정량을 구하시오

9번 다시
확률변수 \(X\)의 분포가 \(P(X = 1) = θ^2, P(X + 2) = 2θ(1 − θ), P(X = 3) = (1 − θ)^2\)(단, \(0 < θ < 1\)) 이라고 하자. 이제 세 개의 관찰값 \(2,2,3\)을 얻었을 때 모수 \(θ\)의 최대가능도 추정값은?
\(f(x) = x \theta^{3-x}(1-\theta)^{x-1}\)
\(L(\theta) = 2\theta(1-\theta) \times 2\theta(1-\theta) \times (1-\theta)^2 = 4\theta^2(1-\theta)^4\)
\(L'(\theta) = 8 \theta(1-\theta)^4 - 16\theta^2(1-\theta)^3) = 8\theta(1-\theta)^3(1-3\theta)=8\theta(1-\theta)^3(1-3\theta) = 0\)
\(\theta=\dfrac{1}{3}\)일 때 \(L(\theta)\)가 최대
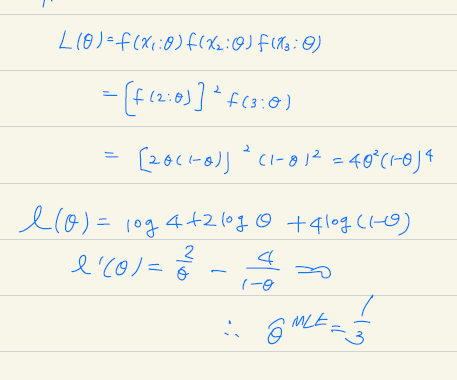
10번
\(X_1, X_2,\dots , X_n\)이 평균이 \(µ\)이고 분산이 \(σ^2\)인 분포로부터 얻은 랜더표본이라고 할 때 모평균 \(µ\)가 알려져 있다면, \(\dfrac{1}{n} \sum_{i=1}^n(X_i − µ)^2\) 이 \(σ^2\)의 비편향 추정량임을 보이시오.
\(E(\dfrac{1}{n} \sum_{i=1}(X_i-\mu)^2) = \dfrac{n\sigma^2}{n} = \sigma^2\)

11번
\(X_1, X_2, \dots, X_n\)이 \(U(−θ, θ), θ > 0\)로부터의 랜덤표본일 때 \(c(X_{(n)} − X_{(1)})\)이 모수 \(θ\)의 비편향 추정량이 되기 위한 상수 \(c\)의 값은?
