DV 3주차(1)

MATPLOTLIB
Author

김보람

Published

September 19, 2022

import matplotlib.pyplot as plt
import numpy as np

Line plot

기본플랏

- 예시

x=[1,2,3,4]
y=[1,2,4,3]
plt.plot(x,y)

모양변경

- 예시1

plt.plot(x,y,'--') #점선

- 예시2

plt.plot(x,y,':')

- 예시3

plt.plot(x,y,'-.')

색상변경

- 예시1

plt.plot(x,y,'r')

- 예시2

plt.plot(x,y,'k') #블랙

모양 + 색상변경

- 예시1

plt.plot(x,y,'--r')  # r을 앞에 쓰든 뒤에 쓰든 나온다

원리?

- r-- 등의 옵션은 Markers + Line Styles + Colors의 조합으로 표현 가능

ref : https://matplotlib.org/stable/api/_as_gen/matplotlib.pyplot.plot.html

  • --r: 점선(dashed)스타일 + 빨간색

  • r--: 빨간색 + 점선(dashed)스타일

  • :k: 점선(dotted)스타일 + 검은색

  • k:: 검은색 + 점선(dotted)스타일

- 우선 Marker를 무시하면 Line Styles + Color로 표현가능한 조합은 4*8 = 32개

(Line Styles) 모두 4개

character description
‘-’ solid line style
‘–’ dashed line style
‘-.’ dash-dot line style
‘:’ dotted line style

(Color) 모두 8개

character color
‘b’ blue
‘g’ green
‘r’ red
‘c’ cyan
‘m’ magenta
‘y’ yellow
‘k’ black
‘w’ white

- 예시1

plt.plot(x,y,'--m')

- 예시2

plt.plot(x,y,'-.c')

- 예시3: line style + color 조합으로 사용하든 color + line style 조합으로 사용하든 상관없음

plt.plot(x,y,'c-.')

- 예시4: line style을 중복으로 사용하거나 color를 중복으로 쓸 수 는 없다.

plt.plot(x,y,'--:')
ValueError: Illegal format string "--:"; two linestyle symbols

plt.plot(x,y,'rb')
ValueError: Illegal format string "rb"; two color symbols

- 예시5: 색이 사실 8개만 있는 것은 아니다.

ref: https://matplotlib.org/2.0.2/examples/color/named_colors.html

plt.plot(x,y,'--',color='aqua') # 8가지 색 외의 다른 것은 color= 옵션으로 줘야함

- 예시6: 색을 바꾸려면 Hex코드를 밖아 넣는 방법이 젤 깔끔함

ref: https://htmlcolorcodes.com/

plt.plot(x,y,color='#277E41')

- 예시7: 라인스타일도 4개만 있지 않다

ref: https://matplotlib.org/stable/gallery/lines_bars_and_markers/linestyles.html

plt.plot(x,y,linestyle='dashed')

plt.plot(x,y,linestyle=(0, (20, 5)))

plt.plot(x,y,linestyle=(0, (20, 1)))

Scatter plot

원리

- 그냥 마커를 설정하면 끝

ref: https://matplotlib.org/stable/api/_as_gen/matplotlib.pyplot.plot.html

character description
‘.’ point marker
‘,’ pixel marker
‘o’ circle marker
‘v’ triangle_down marker
‘^’ triangle_up marker
‘<’ triangle_left marker
‘>’ triangle_right marker
‘1’ tri_down marker
‘2’ tri_up marker
‘3’ tri_left marker
‘4’ tri_right marker
‘8’ octagon marker
‘s’ square marker
‘p’ pentagon marker
‘P’ plus (filled) marker
’*’ star marker
‘h’ hexagon1 marker
‘H’ hexagon2 marker
‘+’ plus marker
‘x’ x marker
‘X’ x (filled) marker
‘D’ diamond marker
‘d’ thin_diamond marker
‘|’ vline marker
’_’ hline marker 
plt.plot(x,y,'o')

기본플랏

plt.plot(x,y,'.')

plt.plot(x,y,'x')

색깔변경

plt.plot(x,y,'or')

plt.plot(x,y,'db')

plt.plot(x,y,'bx')

dot-connected plot

- 예시1: 마커와 라인스타일을 동시에 사용하면 dot-connected plot이 된다.

plt.plot(x,y,'o-')

- 예시2: 당연히 색도 적용가능

plt.plot(x,y,'o--r')

- 예시3: 서로 순서를 바꿔도 상관없다.

plt.plot(x,y,'r--o')

plt.plot(x,y,'ro--')

여러 그림 그리기

겹쳐그리기

- 예시1

x = np.arange(-5,5,0.1)
ϵ = np.random.randn(100)
y = 2*x + ϵ
plt.plot(x,y,'.b')
plt.plot(x,2*x,'r')

따로그리기(subplot) // 외우기

- 예시1

fig, axs = plt.subplots(2)
axs[0].plot(x,y,'.b')
axs[1].plot(x,2*x,'r')

- 예시2

fig, axs = plt.subplots(2,2)
axs[0,0].plot(x,2*x,'--b')
axs[0,1].plot(x,ϵ,'.r')
axs[1,0].plot(x,y,'.r')
axs[1,1].plot(x,y,'.r')
axs[1,1].plot(x,2*x,'-b')

fig와 axes의 이해: matplotlib으로 어렵게 그림을 기리는 방법

예제1

- 목표: plt.plot()을 이용하지 않고 아래의 그림을 그려보자.

plt.plot([1,2,3,4],[1,2,4,3],'or--')

- 구조: axis \(\subset\) axes \(\subset\) figure

ref: https://matplotlib.org/stable/gallery/showcase/anatomy.html#sphx-glr-gallery-showcase-anatomy-py

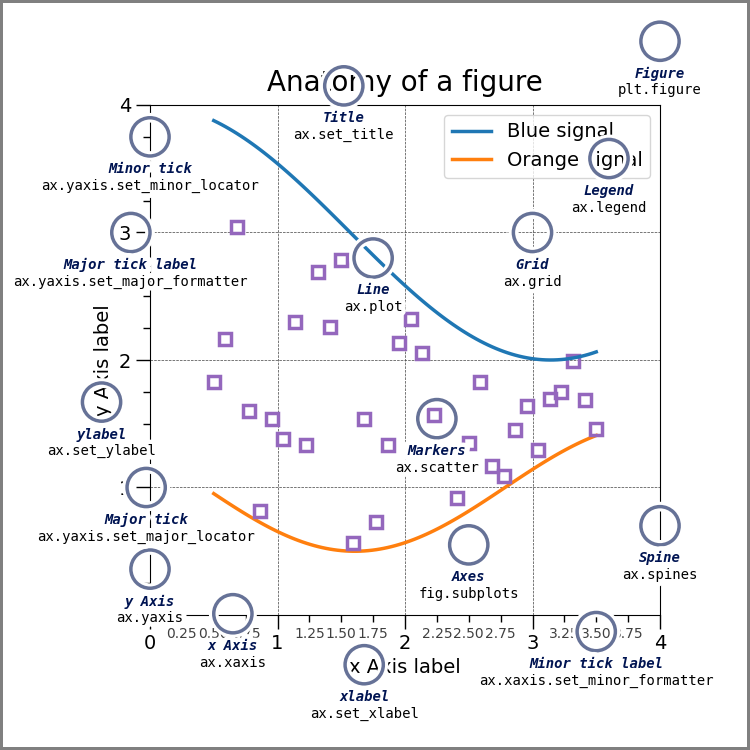
- 전략: Fig을 만들고 (도화지를 준비) \(\to\) axes를 만들고 (네모틀) \(\to\) axes에 그림을 그린다.

- 그림객체를 생성한다.

fig = plt.figure()
<Figure size 432x288 with 0 Axes>
fig # 지금은 아무것도 없다
<Figure size 432x288 with 0 Axes>

- 그림객체에는 여러 인스턴스+함수가 있는데 그중에서 axes도 있다. (그런데 그 와중에 plot method는 없다.)

fig.axes   # 비어있는 리스트
[]

- axes추가

fig.add_axes([0,0,1,1])  # (0,0) 위치에 (1,1)인 액시즈(=네모틀)을 만들어라.
<Axes:>
fig.axes
[<Axes:>]
fig  # 아까는 아무것도 없었는데 지금 도화지안에 네모틀이 들어가 있다.

- 첫번째 액시즈를 ax1으로 받음 (원래 axes1이어야하는데 그냥 편의상)

ax1 = fig.axes[0]
id(fig.axes[0]), id(ax1)
(140307253185296, 140307253185296)

- 잠깐만! (fig오브젝트와 ax1 오브젝트는 포함관계에 있다.)

id(fig.axes[0]), id(ax1)
(140307253185296, 140307253185296)

- 또 잠깐만! (fig오브젝트에는 plot이 없지만 ax1에서는 plot가 있다.)

set(dir(fig)) & {'plot'}
set()
set(dir(ax1)) & {'plot'}
{'plot'}

- ax1.plot()을 사용하여 그림을 그려보자.

ax1.plot([1,2,3,4],[1,2,4,3],'--or') # 안되누?
fig

예제2: 예제1의 응용

- 위에서 축을 하나 더 추가

fig.axes
[<Axes:>]
fig.add_axes([1,1,1,1,])  # (1,1) 위치에 (1,1)크기의 액자틀 추가
<Axes:>
fig.axes  #추가해서 두개
[<Axes:>, <Axes:>]
fig

ax1, ax2 = fig.axes

- ax2에 파란선으로 그림을 그리자

ax2.plot([1,2,3,4],[1,2,4,3],'--ob')
fig

예제3: 응용(미니맵)

- 위의 상황에서 액시지를 하나 더 추가

fig.add_axes([0.65,0.1,0.3,0.3])
<Axes:>
fig

fig.axes[-1].plot([1,2,3,4],[1,2,4,3],'xr')
fig

예제4: 재해석1

(ver1)

plt.plot([1,2,3,4],[1,2,4,3])

(ver2)

ver1은 사실 아래가 연속적으로 실행된 축약구문임

fig = plt.figure() 
fig.add_axes([?,?,?,?])
ax1 = fig.axes[0]
ax1.plot([1,2,3,4],[1,2,4,3])
fig

예제5: 재해석2

fig, axs = plt.subplots(2,2)

fig, axs = plt.subplots(2,2)
axs[0,0].plot([1,2,3,4],[1,2,4,3],'.')
axs[0,1].plot([1,2,3,4],[1,2,4,3],'--r')
axs[1,0].plot([1,2,3,4],[1,2,4,3],'o--')
axs[1,1].plot([1,2,3,4],[1,2,4,3],'o--',color='lime')

- fig, axs = plt.subplots(2,2)의 축약버전을 이해하면된다.

(ver1)

fig, axs = plt.subplots(2,2)

(ver2)

ver1은 사실 아래가 연속적으로 실행된 축약구문임

fig = plt.figure()
fig.add_axes([?,?,?,?]) 
fig.add_axes([?,?,?,?])
fig.add_axes([?,?,?,?])
fig.add_axes([?,?,?,?])
ax1,ax2,ax3,ax4 = fig.axes
axs = np.array(((ax1,ax2),(ax3,ax4)))

(ver3)

ver1은 아래와 같이 표현할 수도 있다.

fig = plt.figure()
axs = fig.subplots(2,2)

숙제

숙제1

fig, axs = plt.subplots(2,3)
axs[0,0].plot([1,2,3,4],[1,2,4,3],'or')
axs[0,1].plot([1,2,3,4],[1,2,4,3],'og')
axs[0,2].plot([1,2,3,4],[1,2,4,3],'ob')
axs[1,0].plot([1,2,3,4],[1,2,4,3],'or--')
axs[1,1].plot([1,2,3,4],[1,2,4,3],'og--')
axs[1,2].plot([1,2,3,4],[1,2,4,3],'ob--')

숙제2

x,y = [1,2,3,4], [1,2,1,1]
fig = plt.figure()
<Figure size 432x288 with 0 Axes>
fig
<Figure size 432x288 with 0 Axes>
fig.axes
[]
fig.add_axes([0,0,1,1]) 
<Axes:>
fig.axes
[<Axes:>]
fig

ax1 = fig.axes[0]
ax1.plot(x,y,'or')
fig

fig.add_axes([0.5,0.5,1,1,])
<Axes:>
fig

fig.add_axes([1,1,1,1,])
<Axes:>
fig

ax1, ax2, ax3 = fig.axes
ax2.plot(x,y,'og')
ax3.plot(x,y,'ob')
fig

숙제3

x = np.arange(-5,5,0.1)
y1 = np.sin(x)
y2 = np.sin(2*x) + 2
y3 = np.sin(4*x) + 4 
y4 = np.sin(8*x) + 6
plt.plot(x, y1, '--r')
plt.plot(x, y2, '--b')
plt.plot(x, y3, '--g')
plt.plot(x, y4, '--m')