[ARA] CH0607 선형회귀분석

Author

김보람

Published

November 14, 2022

해당 강의노트는 전북대학교 이영미교수님 2022-2 고급회귀분석론 자료임

library(MASS)
data(Boston)
head(Boston)
#보스턴 집값 데이터 이 데이터는 보스턴 근교 지역의 집값 및 다른 정보를 포함한다.
#MASS 패키지를 설치하면 데이터를 로딩할 수 있다.
A data.frame: 6 × 14
crim zn indus chas nox rm age dis rad tax ptratio black lstat medv
<dbl> <dbl> <dbl> <int> <dbl> <dbl> <dbl> <dbl> <int> <dbl> <dbl> <dbl> <dbl> <dbl>
1 0.00632 18 2.31 0 0.538 6.575 65.2 4.0900 1 296 15.3 396.90 4.98 24.0
2 0.02731 0 7.07 0 0.469 6.421 78.9 4.9671 2 242 17.8 396.90 9.14 21.6
3 0.02729 0 7.07 0 0.469 7.185 61.1 4.9671 2 242 17.8 392.83 4.03 34.7
4 0.03237 0 2.18 0 0.458 6.998 45.8 6.0622 3 222 18.7 394.63 2.94 33.4
5 0.06905 0 2.18 0 0.458 7.147 54.2 6.0622 3 222 18.7 396.90 5.33 36.2
6 0.02985 0 2.18 0 0.458 6.430 58.7 6.0622 3 222 18.7 394.12 5.21 28.7

B보스턴 근교 506개 지역에 대한 범죄율 (crim)등 14개의 변수로 구성

• crim : 범죄율

• zn: 25,000평방비트 기준 거지주 비율

• indus: 비소매업종 점유 구역 비율

• chas: 찰스강 인접 여부 (1=인접, 0=비인접)

• nox: 일산화질소 농도 (천만개 당)

• rm: 거주지의 평균 방 갯수 ***

• age: 1940년 이전에 건축된 주택의 비율

• dis: 보스턴 5대 사업지구와의 거리

• rad: 고속도로 진입용이성 정도

• tax: 재산세율 (10,000달러 당)

• ptratio: 학생 대 교사 비율

• black: 1000(B − 0.63)2, B: 아프리카계 미국인 비율

• lstat : 저소득층 비율 ****

• medv: 주택가격의 중앙값 (단위:1,000달러 당)

pairs(Boston[,which(names(Boston) %in% c('medv', 'rm', 'lstat'))], pch=16, col='darkorange')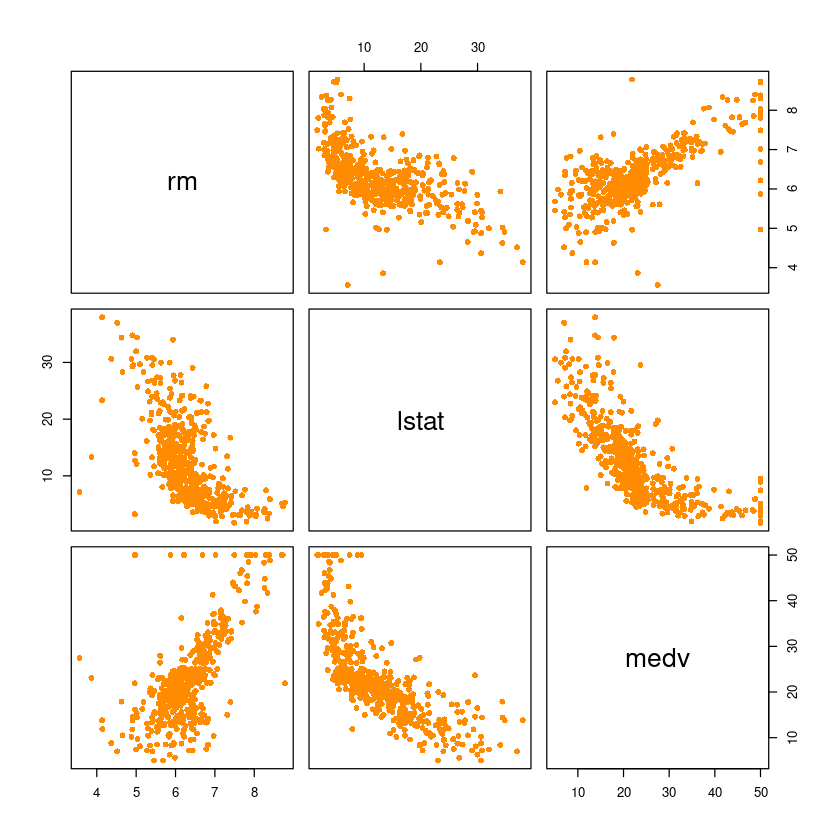

fit_Boston<-lm(medv~rm+lstat, data=Boston)
summary(fit_Boston)

Call:
lm(formula = medv ~ rm + lstat, data = Boston)

Residuals:
    Min      1Q  Median      3Q     Max 
-18.076  -3.516  -1.010   1.909  28.131 

Coefficients:
            Estimate Std. Error t value Pr(>|t|)    
(Intercept) -1.35827    3.17283  -0.428    0.669    
rm           5.09479    0.44447  11.463   <2e-16 ***
lstat       -0.64236    0.04373 -14.689   <2e-16 ***
---
Signif. codes:  0 ‘***’ 0.001 ‘**’ 0.01 ‘*’ 0.05 ‘.’ 0.1 ‘ ’ 1

Residual standard error: 5.54 on 503 degrees of freedom
Multiple R-squared:  0.6386,    Adjusted R-squared:  0.6371 
F-statistic: 444.3 on 2 and 503 DF,  p-value: < 2.2e-16
dt <- Boston[,which(names(Boston) %in% c('medv', 'rm', 'lstat'))]
head(dt)
A data.frame: 6 × 3
rm lstat medv
<dbl> <dbl> <dbl>
1 6.575 4.98 24.0
2 6.421 9.14 21.6
3 7.185 4.03 34.7
4 6.998 2.94 33.4
5 7.147 5.33 36.2
6 6.430 5.21 28.7 
fit_Boston<-lm(medv~., data=dt)
anova(fit_Boston)
vcov(fit_Boston)  ##var(hat beta) = (X^TX)^-1 \sigma^2
A anova: 3 × 5
Df Sum Sq Mean Sq F value Pr(>F)
<int> <dbl> <dbl> <dbl> <dbl>
rm 1 20654.42 20654.41622 672.9039 8.266887e-95
lstat 1 6622.57 6622.56999 215.7579 6.669365e-41
Residuals 503 15439.31 30.69445 NA NA
A matrix: 3 × 3 of type dbl
(Intercept) rm lstat
(Intercept) 10.06683612 -1.39248641 -0.099178133
rm -1.39248641 0.19754958 0.011930670
lstat -0.09917813 0.01193067 0.001912441 
confint(fit_Boston, level = 0.95)
A matrix: 3 × 2 of type dbl
2.5 % 97.5 %
(Intercept) -7.5919003 4.8753547
rm 4.2215504 5.9680255
lstat -0.7282772 -0.5564395 
coef(fit_Boston) + qt(0.975, 503) * summary(fit_Boston)$coef[,2]
coef(fit_Boston) - qt(0.975, 503) * summary(fit_Boston)$coef[,2]
(Intercept)
4.87535465808391
rm
5.9680255329079
lstat
-0.556439501179164
(Intercept)
-7.59190028183295
rm
4.22155043576519
lstat
-0.728277167309094
############# 평균반응, 개별 y 추정
## E(Y|x0), y = E(Y|x0) + epsilon
new_dt <- data.frame(rm=7, lstat=10)
# hat y0 = -1.3583 + 5.0948*7 - 0.6424*10
predict(fit_Boston, newdata = new_dt)
1: 27.88165973604 
predict(fit_Boston, 
        newdata = new_dt,
        interval = c("confidence"), 
        level = 0.95)  ##평균반응
A matrix: 1 × 3 of type dbl
fit lwr upr
1 27.88166 27.17347 28.58985 
predict(fit_Boston, newdata = new_dt, 
        interval = c("prediction"), 
        level = 0.95)  ## 개별 y
A matrix: 1 × 3 of type dbl
fit lwr upr
1 27.88166 16.97375 38.78957 

############ 잔차분석 
### epsilon : 선형성, 등분산성, 정규성, 독립성 

yhat <- fitted(fit_Boston)
res <- resid(fit_Boston)

plot(res ~ yhat,pch=16, ylab = 'Residual')
abline(h=0, lty=2, col='grey')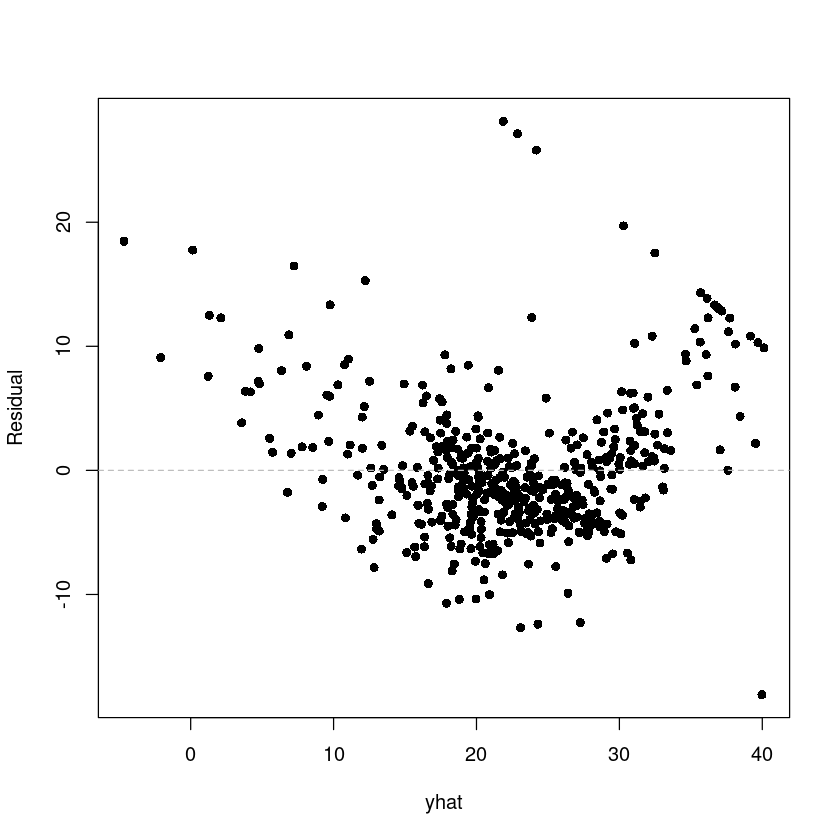

plot(res ~ dt$rm,pch=16, ylab = 'Residual')
abline(h=0, lty=2, col='grey')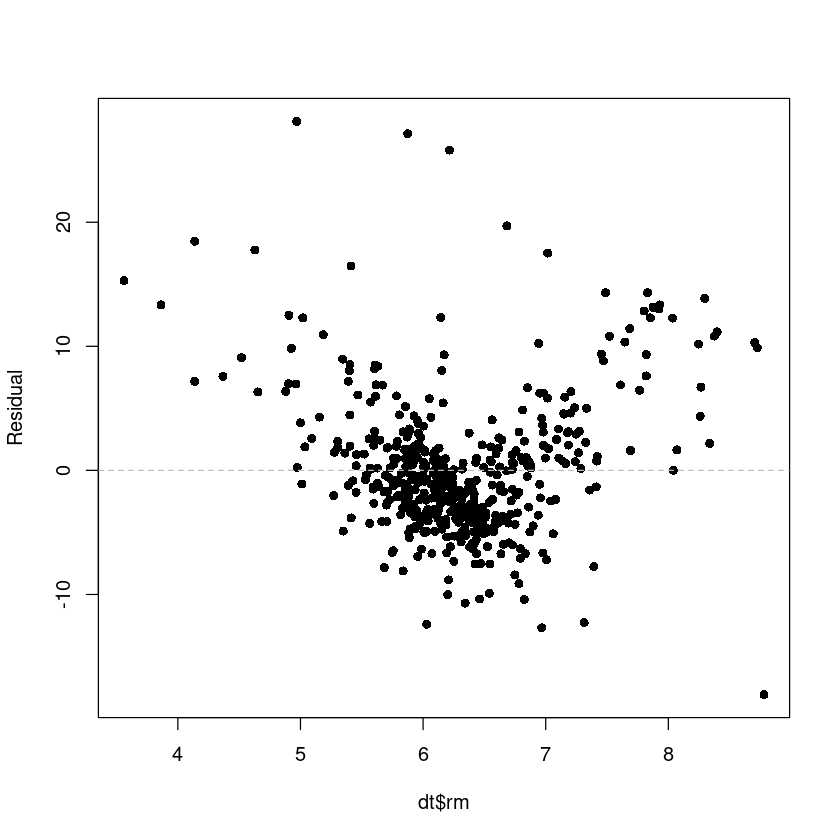

plot(res ~ dt$lstat,pch=16, ylab = 'Residual')
abline(h=0, lty=2, col='grey')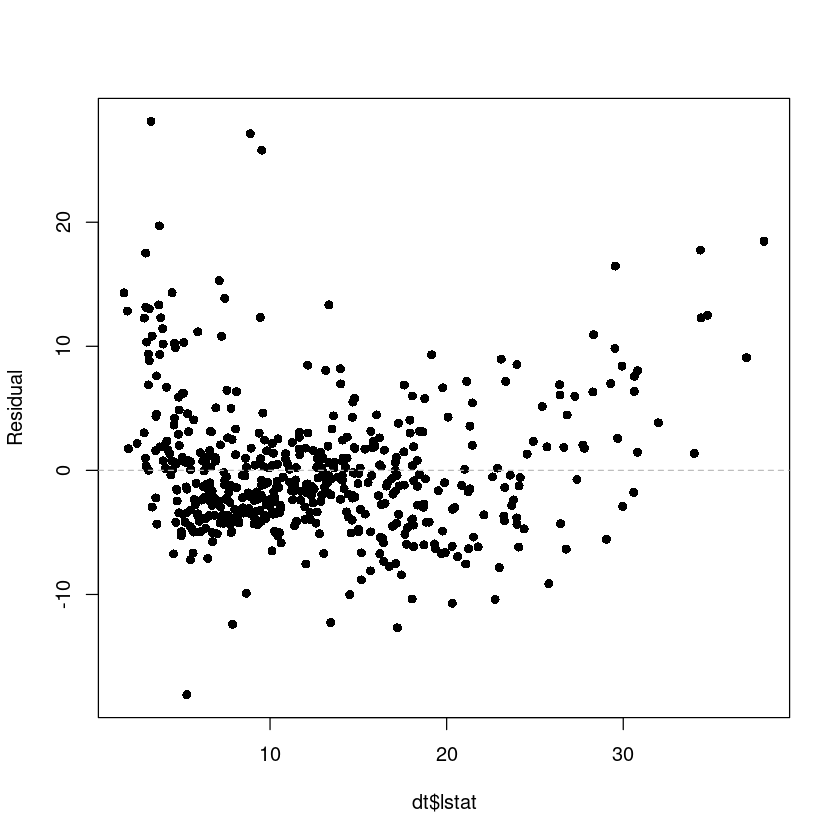

# 독립성검정 : DW test
library(lmtest)
## 
dwtest(fit_Boston, alternative = "two.sided")  #H0 : uncorrelated vs H1 : rho != 0
Loading required package: zoo


Attaching package: ‘zoo’


The following objects are masked from ‘package:base’:

    as.Date, as.Date.numeric



    Durbin-Watson test

data:  fit_Boston
DW = 0.83421, p-value < 2.2e-16
alternative hypothesis: true autocorrelation is not 0
## 잔차의 QQ plot
qqnorm(res, pch=16)
qqline(res, col = 2)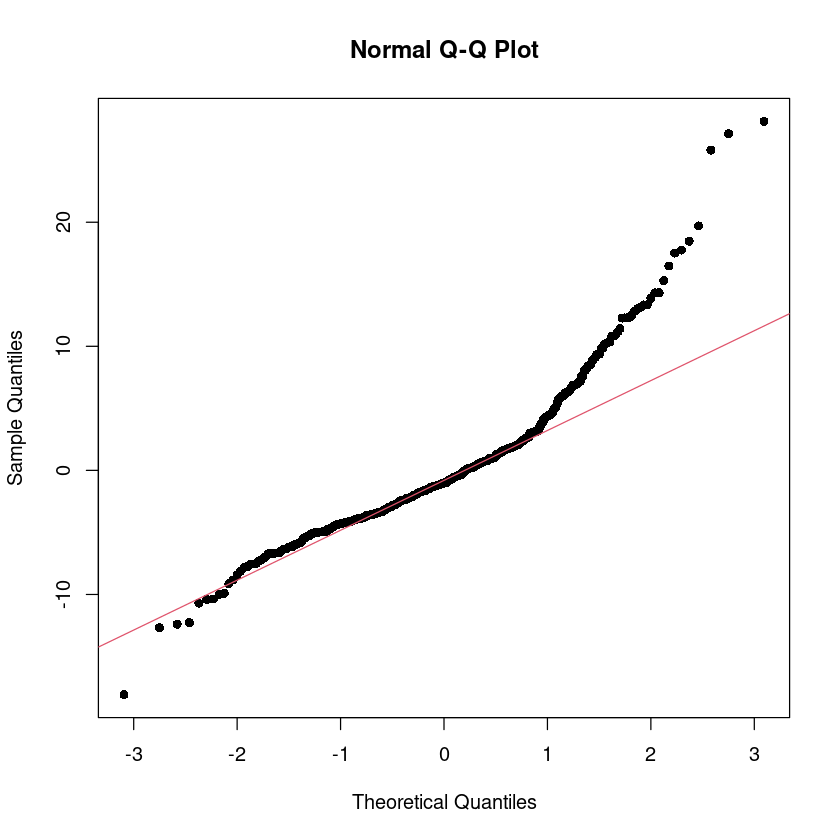

head(dt)
dt$lstat2 <- (dt$lstat)^2
head(dt)
fit_Boston2<-lm(medv~., data=dt)
A data.frame: 6 × 3
rm lstat medv
<dbl> <dbl> <dbl>
1 6.575 4.98 24.0
2 6.421 9.14 21.6
3 7.185 4.03 34.7
4 6.998 2.94 33.4
5 7.147 5.33 36.2
6 6.430 5.21 28.7
A data.frame: 6 × 4
rm lstat medv lstat2
<dbl> <dbl> <dbl> <dbl>
1 6.575 4.98 24.0 24.8004
2 6.421 9.14 21.6 83.5396
3 7.185 4.03 34.7 16.2409
4 6.998 2.94 33.4 8.6436
5 7.147 5.33 36.2 28.4089
6 6.430 5.21 28.7 27.1441 
fit_Boston2<-lm(medv~rm+lstat+I(lstat^2), data=Boston)
summary(fit_Boston2)

Call:
lm(formula = medv ~ rm + lstat + I(lstat^2), data = Boston)

Residuals:
     Min       1Q   Median       3Q      Max 
-18.1427  -3.2429  -0.4829   2.3607  27.0256 

Coefficients:
            Estimate Std. Error t value Pr(>|t|)    
(Intercept) 11.68964    3.13810   3.725 0.000217 ***
rm           4.22727    0.41172  10.267  < 2e-16 ***
lstat       -1.84863    0.12213 -15.136  < 2e-16 ***
I(lstat^2)   0.03634    0.00348  10.443  < 2e-16 ***
---
Signif. codes:  0 ‘***’ 0.001 ‘**’ 0.01 ‘*’ 0.05 ‘.’ 0.1 ‘ ’ 1

Residual standard error: 5.027 on 502 degrees of freedom
Multiple R-squared:  0.7031,    Adjusted R-squared:  0.7013 
F-statistic: 396.2 on 3 and 502 DF,  p-value: < 2.2e-16

yhat2 <- fitted.values(fit_Boston2)
res2 <- resid(fit_Boston2)

plot(res2 ~ yhat2,pch=16, ylab = 'Residual')
abline(h=0, lty=2, col='grey')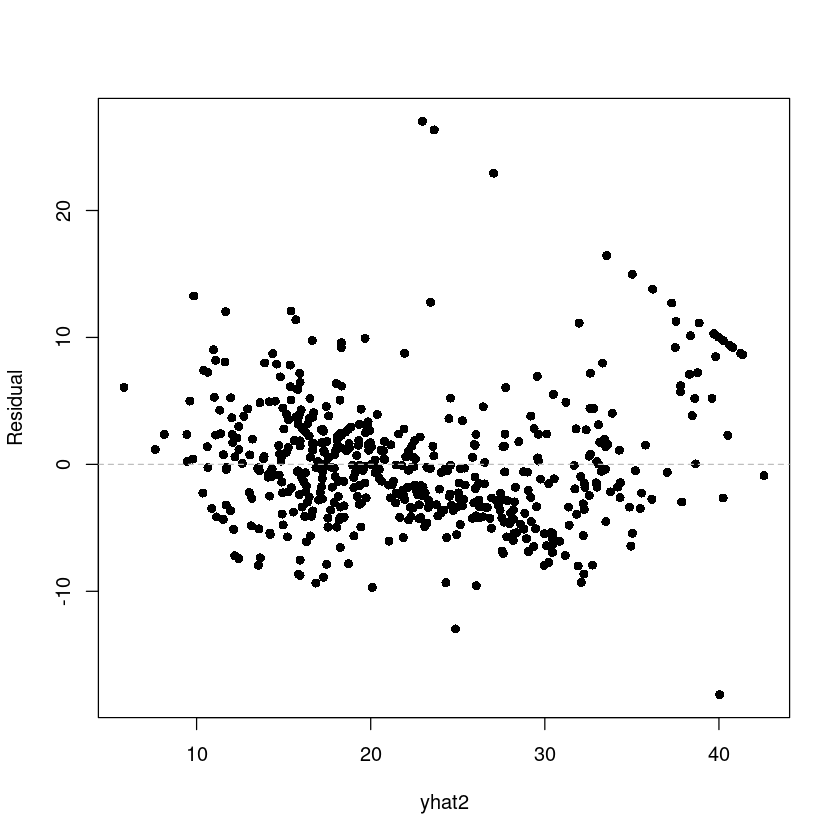

qqnorm(res2, pch=16)
qqline(res2, col = 2)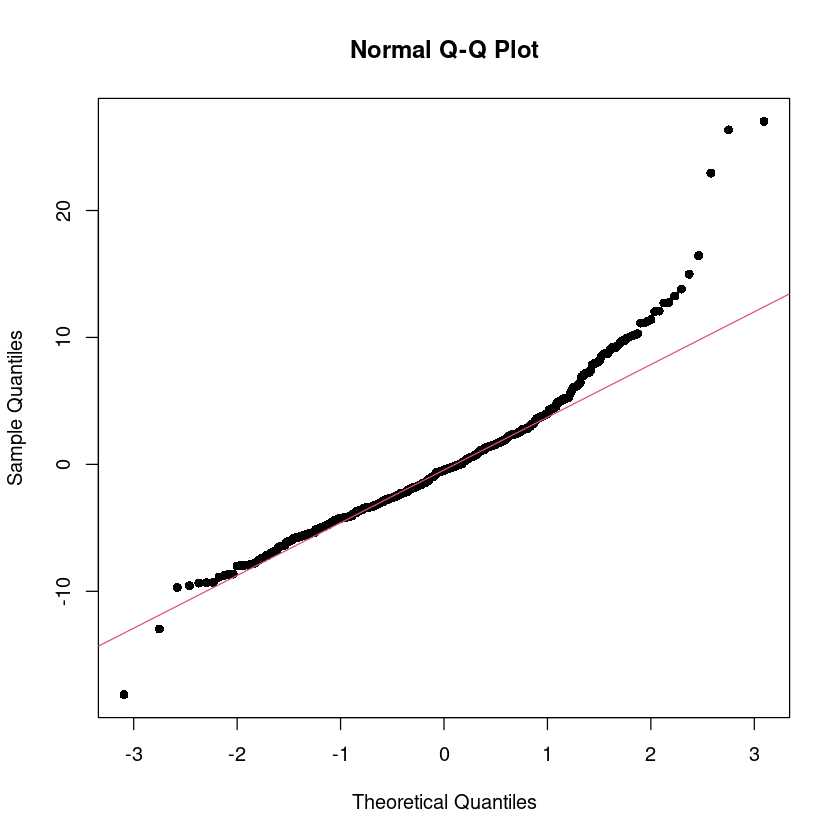

dwtest(fit_Boston2, alternative = "two.sided")  #H0 : uncorrelated vs H1 : rho != 0

    Durbin-Watson test

data:  fit_Boston2
DW = 0.84831, p-value < 2.2e-16
alternative hypothesis: true autocorrelation is not 0
fit_Boston3 <- lm(medv~rm, data=Boston)
fit_Boston4 <- lm(medv~lstat, data=Boston)
summary(fit_Boston3)

Call:
lm(formula = medv ~ rm, data = Boston)

Residuals:
    Min      1Q  Median      3Q     Max 
-23.346  -2.547   0.090   2.986  39.433 

Coefficients:
            Estimate Std. Error t value Pr(>|t|)    
(Intercept)  -34.671      2.650  -13.08   <2e-16 ***
rm             9.102      0.419   21.72   <2e-16 ***
---
Signif. codes:  0 ‘***’ 0.001 ‘**’ 0.01 ‘*’ 0.05 ‘.’ 0.1 ‘ ’ 1

Residual standard error: 6.616 on 504 degrees of freedom
Multiple R-squared:  0.4835,    Adjusted R-squared:  0.4825 
F-statistic: 471.8 on 1 and 504 DF,  p-value: < 2.2e-16
summary(fit_Boston4)

Call:
lm(formula = medv ~ lstat, data = Boston)

Residuals:
    Min      1Q  Median      3Q     Max 
-15.168  -3.990  -1.318   2.034  24.500 

Coefficients:
            Estimate Std. Error t value Pr(>|t|)    
(Intercept) 34.55384    0.56263   61.41   <2e-16 ***
lstat       -0.95005    0.03873  -24.53   <2e-16 ***
---
Signif. codes:  0 ‘***’ 0.001 ‘**’ 0.01 ‘*’ 0.05 ‘.’ 0.1 ‘ ’ 1

Residual standard error: 6.216 on 504 degrees of freedom
Multiple R-squared:  0.5441,    Adjusted R-squared:  0.5432 
F-statistic: 601.6 on 1 and 504 DF,  p-value: < 2.2e-16
x1<-c(4,8,9,8,8,12,6,10,6,9)
x2<-c(4,10,8,5,10,15,8,13,5,12)
y<-c(9,20,22,15,17,30,18,25,10,20)
fit<-lm(y~x1+x2)  ##FM
summary(fit)

Call:
lm(formula = y ~ x1 + x2)

Residuals:
    Min      1Q  Median      3Q     Max 
-2.4575 -1.9100  0.3314  0.6388  3.2628 

Coefficients:
            Estimate Std. Error t value Pr(>|t|)  
(Intercept)  -0.6507     2.9075  -0.224   0.8293  
x1            1.5515     0.6462   2.401   0.0474 *
x2            0.7599     0.3968   1.915   0.0970 .
---
Signif. codes:  0 ‘***’ 0.001 ‘**’ 0.01 ‘*’ 0.05 ‘.’ 0.1 ‘ ’ 1

Residual standard error: 2.278 on 7 degrees of freedom
Multiple R-squared:  0.9014,    Adjusted R-squared:  0.8732 
F-statistic:    32 on 2 and 7 DF,  p-value: 0.0003011
anova(fit)
A anova: 3 × 5
Df Sum Sq Mean Sq F value Pr(>F)
<int> <dbl> <dbl> <dbl> <dbl>
x1 1 313.04348 313.043478 60.323103 0.0001100467
x2 1 19.03040 19.030400 3.667135 0.0970444465
Residuals 7 36.32612 5.189446 NA NA 
# install.packages("car")
library(car)
Loading required package: carData


## H0 : T*beta = c 


#b1-b2=0 => (0,1,-1) *beta 
#H_0 : beta_1 = beta2
linearHypothesis(fit, c(0,1,-1), 0)
A anova: 2 × 6
Res.Df RSS Df Sum of Sq F Pr(>F)
<dbl> <dbl> <dbl> <dbl> <dbl> <dbl>
1 8 39.53514 NA NA NA NA
2 7 36.32612 1 3.209014 0.6183731 0.4574425 
#H_0 : beta_1 = 1
linearHypothesis(fit, c(0,1,0), 1)
A anova: 2 × 6
Res.Df RSS Df Sum of Sq F Pr(>F)
<dbl> <dbl> <dbl> <dbl> <dbl> <dbl>
1 8 40.10492 NA NA NA NA
2 7 36.32612 1 3.778797 0.7281696 0.4217136 
#H_0 : beta_1 = beta2 + 1
linearHypothesis(fit, c(0,1,-1), 1)
A anova: 2 × 6
Res.Df RSS Df Sum of Sq F Pr(>F)
<dbl> <dbl> <dbl> <dbl> <dbl> <dbl>
1 8 36.54865 NA NA NA NA
2 7 36.32612 1 0.2225273 0.04288074 0.841845 
##H_0 : beta_1 = beta2 + 1
#y=b0 + b1x1 + b2x2 + e = b0+x1 + b2(x1+x2)+e
#y-x1 = b0+b2(x1+x2)+e :   RM

y1 <- y-x1
z1 <- x1 + x2
fit2 <- lm(y1~z1)
summary(fit2)
anova(fit2)

Call:
lm(formula = y1 ~ z1)

Residuals:
    Min      1Q  Median      3Q     Max 
-2.5054 -1.9294  0.4236  0.6821  3.4473 

Coefficients:
            Estimate Std. Error t value Pr(>|t|)    
(Intercept)  -1.0014     2.2175  -0.452 0.663574    
z1            0.6824     0.1242   5.493 0.000578 ***
---
Signif. codes:  0 ‘***’ 0.001 ‘**’ 0.01 ‘*’ 0.05 ‘.’ 0.1 ‘ ’ 1

Residual standard error: 2.137 on 8 degrees of freedom
Multiple R-squared:  0.7904,    Adjusted R-squared:  0.7642 
F-statistic: 30.17 on 1 and 8 DF,  p-value: 0.0005785
A anova: 2 × 5
Df Sum Sq Mean Sq F value Pr(>F)
<int> <dbl> <dbl> <dbl> <dbl>
z1 1 137.85135 137.851351 30.17378 0.0005784583
Residuals 8 36.54865 4.568581 NA NA 
anova(fit)  ##FM
anova(fit2)  #RM
A anova: 3 × 5
Df Sum Sq Mean Sq F value Pr(>F)
<int> <dbl> <dbl> <dbl> <dbl>
x1 1 313.04348 313.043478 60.323103 0.0001100467
x2 1 19.03040 19.030400 3.667135 0.0970444465
Residuals 7 36.32612 5.189446 NA NA
A anova: 2 × 5
Df Sum Sq Mean Sq F value Pr(>F)
<int> <dbl> <dbl> <dbl> <dbl>
z1 1 137.85135 137.851351 30.17378 0.0005784583
Residuals 8 36.54865 4.568581 NA NA 
# F = {(SSE_RM - SSE_FM)/r} / {SSE_FM/(n-p-1)}
SSE_FM <- anova(fit)$Sum[3]  #SSE_FM
SSE_RM <- anova(fit2)$Sum[2]  #SSE_RM
F0 <- (SSE_RM-SSE_FM)/(SSE_FM/7)
F0
0.0428807391894599 
#기각역 F_{0.05}(1,7)
qf(0.95, 1, 7)
5.59144785122073