[GNN] 논문 정리 (~ing)

GNN
Author

김보람

Published

July 18, 2023

GNN으로 할 수 있는 것

  1. Node Classification
  • Node embedding을 통해 점 분류 (인용 네트워크, Reddit게시물, Youtube동영상)
  1. Link Prediction
  • 그래프 점들 사이에 관계 파악 및 두 점 사이 연관성 예측
  1. Graph Classification
  • 그래프 전체 여러가지 카테고리로 분류

GNN변천사

출처: https://tootouch.github.io/research/gnn_summary/

https://arxiv.org/pdf/1901.00596.pdf

GCN

REF

https://wonbae.github.io/2021-02-26-Graph9-GNN/

https://thejb.ai/comprehensive-gnns-3/ \(\star\)

https://github.com/heartcored98/Standalone-DeepLearning/tree/master

https://ahjeong.tistory.com/15

논문 종류

  1. Recurrent Graph Neural Network

  2. Spatial Convolutional Network

  3. Spectral Convolutional Network

GCN변천사

1

1-1

https://arxiv.org/ftp/arxiv/papers/1812/1812.08434.pdf

Propagation Modeule - Recurrent Operator - Convergence - GNN

Graph neural networks: A review of methods and applications

  • popular platforms for graph computing |Platform|Link|Reference| |—|—|—| |PyTorch Geometric |https://github.com/rusty1s/pytorch_geometric| Fey and Lenssen (2019)| |Deep Graph Library |https://github.com/dmlc/dgl |Wang et al. (2019b)| |AliGraph |https://github.com/alibaba/aligraph |Zhu et al. (2019a)| |GraphVite |https://github.com/DeepGraphLearning/graphvite |Zhu et al. (2019b)| |Paddle Graph Learning |https://github.com/PaddlePaddle/PGL|| |Euler |https://github.com/alibaba/euler|| |Plato |https://github.com/tencent/plato|| |CogDL |https://github.com/THUDM/cogdl/|| |OpenNE h|ttps://github.com/thunlp/OpenNE/tree/pytorch||

1-2

https://ieeexplore.ieee.org/document/4700287

@ARTICLE{4700287,
  author={Scarselli, Franco and Gori, Marco and Tsoi, Ah Chung and Hagenbuchner, Markus and Monfardini, Gabriele},
  journal={IEEE Transactions on Neural Networks}, 
  title={The Graph Neural Network Model}, 
  year={2009},
  volume={20},
  number={1},
  pages={61-80},
  doi={10.1109/TNN.2008.2005605}}

2

2-1

https://arxiv.org/abs/1609.02907

‘Semi-Supervised Classification with Graph Convolutional Networks’

2-2

참고자료

  1. F. Scarselli, M. Gori, “The graph neural network model,” IEEE Transactions on Neural Networks, 2009
  • https://ieeexplore.ieee.org/stamp/stamp.jsp?arnumber=4700287
  1. Z. Wu, S. Pan, F. Chen, G. Long, C. Zhang, Philip S. Yu, “A Comprehensive Survey on Graph Neural Networks”, arXiv:1901.00596
  • https://ieeexplore.ieee.org/stamp/stamp.jsp?arnumber=9046288
  1. T. N. Kipf and M. Welling, “Semi-supervised classification with graph convolutional networks,” in Proc. of ICLR, 2017
  • https://arxiv.org/pdf/1609.02907.pdf%EF%BC%89
  1. J. Gilmer, S. S. Schoenholz, P. F. Riley, O. Vinyals, and G. E. Dahl, “Neural Message Passing for Quantum Chemistry”, in Proc. of ICML, 2017
  • http://proceedings.mlr.press/v70/gilmer17a/gilmer17a.pdf
  • 이건 화학적 분자구조를 뉴럴로 한거같은데,, 약간 참고자료용??
  1. D. Xu, Y. Zhu, C. B. Choy, and L. Fei-Fei, “Scene graph generation by iterative message passing,” in Proc. of CVPR, 2017
  • https://openaccess.thecvf.com/content_cvpr_2017/papers/Xu_Scene_Graph_Generation_CVPR_2017_paper.pdf
  • 시각적 기반이 되는 이미지 그래픽 구조
  • 입력 이미지로부터 구조화된 장면 표현하는 모델
  1. J. Johnson, A. Gupta, and L. Fei-Fei, “Image generation from scene graphs,” in Proc. of CVPR, 2018
  • 그래프 모델을 사용한 이미지 생성

  1. D. Teney, L. Liu and A. van den Hengel, “Graph-Structured Representations for Visual Question Answering”, in Proc. of CVPR, 2017

  2. B. Sanchez-Lengeling, J. N. Wei, B. K. Lee, R. C. Gerkin, A. Aspuru-Guzik, and A. B. Wiltschko, “Machine Learning for Scent: Learning Generalizable Perceptual Representations of Small Molecules”, arXiv: 1910.10685

  3. R. van den Berg, T. N. Kipf, and M. Welling, “Graph Convolutional Matrix Completion”, arXiv:1706.02263

Alet, Ferran, et al. “Graph element networks: adaptive, structured computation and memory.” International Conference on Machine Learning. PMLR, 2019.

  • spatial processes가 없는 공간

Allamanis, Miltiadis, Marc Brockschmidt, and Mahmoud Khademi. “Learning to represent programs with graphs.” arXiv preprint arXiv:1711.00740 (2017).

그래프 신경망 입문 도서(Introduction to Graph Neural Networks)

  • 지은이: 즈위안 리우, 지에 저우

1. 그래프 합성곱 네트워크

(1) 스펙트럼 방법(여러 가지 파동들의 집합)

출처: https://tootouch.github.io/research/gnn_summary/

- Spectral Convolutional Neural Network (Spectral CNN) 스펙트럼 네트워크

(Denton, Emily L., et al. “Exploiting linear structure within convolutional networks for efficient evaluation.” Advances in neural information processing systems 27 (2014).)

  • 푸리에 영역에서 그래프 라플라시안의 고유 분해 계산

\[x \in {\mathbb R}, \theta \in {\mathbb R}^N, g_\theta=diah(\theta)\]

\[g_\theta \times x = U_{g_\theta}(\wedge)U^Tx\]

\[L=I_N-D^{-\frac{1}{2}}AD^{-\frac{1}{2}}=U \wedge U^T\]

U: L의 고유벡터로 이루어진 행렬, \(\wedge\): L의 고윳값으로 이뤄진 대각행렬

- Chebyshev Spectral Convolutional Neural Network(ChebNet)

  • 논문링크

  • 거리가 K이하인 범위를 다루는 합성곱을 사용해 합성곱 신경망을 정의함->라플라시안 고유벡터 전부 계산 안해도 된다.

\[g_\theta = \sum_{i=0}^K \theta_i T_i(\tilde \wedge)\]

  • 체비쇼프 다항식

\(T_k(x) = 2xT_{k-1}(x) - T_{k-2}(x)\)

\(T_0(x)=1, T_1(x) = x\)

- Graph Convolutional Network (GCN)

  • (https://arxiv.org/pdf/1706.02263.pdf)

  • https://arxiv.org/abs/1609.02907

  • ChebNet의 식에서 \(K=1, \lambda_{max}=2\)로 근사

\[g_\theta' \times x \approx \theta_0' x + \theta_1'(L-I_N)x = \theta_0' x - \theta_1' D^{-\frac{1}{2}}AD^{-\frac{1}{2}}x\]

  • 위 식에서 \(\theta=\theta_0' = -\theta_1'\) 이라고 가정(오버피팅 방지)

\[g_\theta \times x \approx \theta(I_N + D^{-\frac{1}{2}}AD^{-\frac{1}{2}})x\]

- AGCN

  • Li, Ruoyu, et al. “Adaptive graph convolutional neural networks.” Proceedings of the AAAI conference on artificial intelligence. Vol. 32. No. 1. 2018

(2) 공간 방법

  • 공간적으로 가까운 이웃 노드에 직접 적용하는 합성곱 정의

- 뉴럴 FPS

논문:Convolutional Networks on Graphs for Learning Molecular Fingerprints

다른 차수의 노드에 다른 가중치 행렬 사용

\[x=h_v^{t-1} + \sum_{i=1}^{|N_v|}h_i^{t-1}\]

\[h_v^t = \sigma (x W_t^{|N_v|})\]

\(h_v^t\): t번째 층에서 노드 v의 임베딩

\(N_v\): 노드 v의 이웃 집합

\(W_t^{|N_v|}\): t번째 층에서 차수가 \(|N_V|\)인 노드의 가중치 행렬

차수별로 다른 행렬을 사용하므로ㅗ 노드 차수가 많은 큰 규모의 그래프에서 사용할 수 없다.

- PATCHY-SAN

논문:Learning Convolutional Neural Networks for Graphs

1. 노드 선택

  • 모든 노드에서 단계 진행하지 않고 그래프 레이블링 통해 노드의 순서를 정하고 그 순서를 기반으로 노드를 W개 선택

2. 이웃 모으기

  • 각 단계에서 선택한 노드 각각을 기준으로 수용 영역을 만든다.

  • 너비 우선 선택(breadth-first search)을 통해 k개를 뽑는다.

  • 거리가 1인 노드를 고르고 부족하면 거리를 늘려서 가까운 노드 k개를 고른다.

3. 그래프 정규화

  • 수용 영역에 있는 노드의 순서를 매겨서 순서가 있는 그래프 공간을 벡터 공간으로 바꾼다.

  • \(\star\) 구조적으로 비슷한 역할을 하는 노드는 다른 그래프에 있어도 비슷한 위치로 여긴다.

4. 합성곱 구조

-정규화된 이웃을 수용 영역으로 노드와 에지 속성을 채널로 한다.

- Diffusion-Convolutional Neural Network(DCNN:확산 합성곱 신경망)

논문: Diffusion-Convolutional Neural Networks

추이행렬(transition matrix) 사용: 노드의 이웃 정의

\(P\): 그래프 인접행렬 A로부터 얻은 차수 정규화 추이행렬

\(P*\): 행렬 P의 거듭제곱근수 \(\{P, P^2, \dots, P^K\}\)로 이뤄진 \(N \times K \times N\)(N은 노드수) 텐서

\[H=\sigma(W^c \odot P^*X)\]

\(X\): \(N \times F\)입력 특징 텐서

\(X\)에 \(P^*\)를 곱해서 각 원소는 K홉 그래프 확산을 뜻하는 \(K \times F\) 행렬인 확산 합성곱 표현으로 바뀜

- DGCN

논문: Dual Graph Convolutional Networks for Graph-Based Semi-Supervised Classification

  • 그래프의 부분 일관성과 전체 일관성 모두 고려

  • 합성곱 그래프 2개와 비지도 손실 함수 2개 사용

- 첫번째 합성곱 네트워트

\[Z={\tilde D}^{-\frac{1}{2}}{\tilde A}{\tilde D}^{-\frac{1}{2}}X \Theta\]

\(\tilde A= A+I_N\)

C: 입력 채널 수

\(X \in {\mathbb R}^{N \times C}\): 신호

\(\Theta \in {\mathbb R}^{C \times F}\): 필터 파라미터 행렬

\(Z \in {\mathbb R}^{N \times C}\): 합성곱 적용한 신호 행렬

  • 가까운 노드는 비슷한 레이블을 가질 가능성이 높다는 것을 의미하는 부분 일관성: \(\text{Conv}_A\)

- 두번째 합성곱 네트워크

  • 인접행렬 대신 양의 점별 상호 정보(PPMI:Positive Pointwise Mutual Information) 행렬

\[H'=\sigma(D^{-\frac{1}{2}}_P X_P D_P^{-\frac{1}{2}} H \Theta)\]

\(X_P\): PPMI행렬

\(D_P\): \(X_P\)의 대각행렬

  • 비슷한 내용을 가진 노드는 비슷한 레이블을 가질 가능성이 높다는 것을 의미하는 전체 일관성: \(\text{Conv}_P\)

- 손실 함수1

\[L=L_0(\text{Conv}_A)+\lambda(t)L_{reg}(\text{Conv}_A,\text{Conv}_P)\]

\(\lambda(t)\): 두 손실 함수의 중요성 조절하는 가중치

\(L_0(\text{Conv}_A)\): 주어진 노드 레이블에 대한 지도 손실 함수

  • 크로스 엔트로피 에러를 사용해 \(L_0(\text{Conv}_A)\) 계산

\[L_0(\text{Conv}_A)= -\frac{1}{|y_L|} \sum_{l \in y_L} \sum_{i=1}^c Y_{l,i} ln(\hat Z_{l,i}^A)\]

\(y_L\): 학습 데이터의 인덱스 집합

\(Y\): 정답값

- 손실 함수2

\[L_{reg}(\text{Conv}_A, \text{Conv}_P) = \frac{1}{n} \sum_{i=1}^n ||\hat Z_{i,:}^P - \hat Z_{i,:}^A||^2\]

- 모델 구조

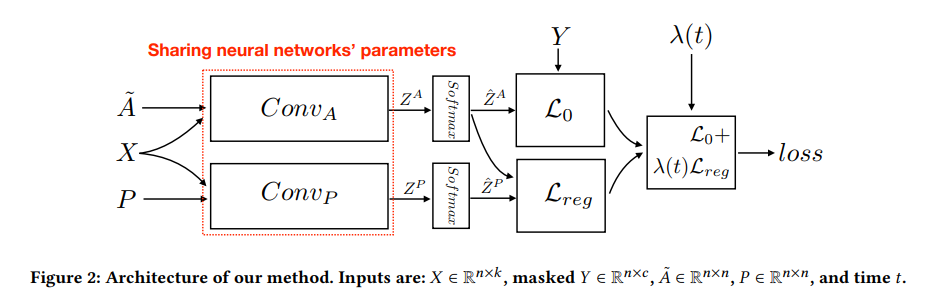
- LGCN

논문:Large-Scale Learnable Graph Convolutional Networks

Learnable Graph Convolutional Network: 학습 가능한 그래프 합성곱 네트워크

https://github.com/HongyangGao/LGCN

:학습 가능한 그래프 합성곱 층(LGCL:Learnable Graph Convolutional Layer)+부분 그래프 합성 전략

- LGCL

  • 관련 높은 k개의 특징 요소를 얻기 위해서 노드의 이웃 행렬에 최대 풀링을 적용 후 1차원 CNN을 적용해 은닉 표현 계산

  • 전파단계

\[\hat H_t = g(H_t, A, k)\]

\[H_{t+1}=c (\hat H_t)\]

\(A\): 인접행렬

\(g()\): 가장 큰 노드 k개 뽑는 연산

\(c()\): 일반적인 1차원 CNN

- 예시

??? 예시를 봐도 잘 모르겠다..

- MoNET

논문:Geometric deep learning on graphs and manifolds using mixture model CNNs

과거 결과들을 일반화하는 모델

- 예시

  • GCNN(geodesic CNN)

  • ACNN(anisotropic CNN)

  • GCN

  • DCNN

- 가중치 함수

\[D_j(x)f = \sum_{y \in N_x} w_j(u(x,y))f(y)\]

노드와 이웃 간의 가짜 좌표 \(u(x,y)\)를 계사나고 이를 이용해 가중치 함수를 정의한다.

노드의 이웃에 각각 가중치를 두는 방법

\(u\)와 \(w(u)\)를 어떻게 정의하는지에 따라 모델을 정의할 수 있다.

- GraphSAGE

논문:Representation learning on graphs: Methods and applications

논문:Inductive representation learning on large graphs

근처에 있는 노드의 특징을 샘플링하고 모아서 임베딩 계산

- 전파 단계

\[h_{N_v}^t = \text{AGGREGATE}_t(\{h_u^{t-1}, \forall u \in N_v \})\]

\[h_v^t = \sigma(W^t \cdot [h_v^{t-1}||h_{N_v}^t])\]

이웃 노드를 모두 사용하지 않고 정해진 개수만 골고루 샘플링

GRN

Gated Graph Neural Network(GGNN:게이트 그래프 신경망)

논문:Gated graph sequence neural networks

https://www.cs.toronto.edu/~yujiali/files/talks/iclr16_ggnn_talk.pdf

https://github.com/chingyaoc/ggnn.pytorch

https://katefvision.github.io/LanguageGrounding/Slides/27.pdf

정해진 횟수에 대한 순환 신경망을 풀고 시간을 통해 역전파해서 그레이디언트 계산

Gated Graph Sequence Neural Network(GGS-NN)

Tree-LSTM

논문:Improved semantic representations from tree-structured long short-term memory networks)

1. Child-Sum Tree-LSTM

\(\tilde h_v^{t-1} = \sum_{k \in N_v} h_k^{t-1}\)

입력 게이트 \(i_v^t = \sigma(W^ix_v^t + U^i {\tilde h_v^{t-1}} + b^i)\)

망각 게이트 \(f^t_{vk} = \sigma(W^f x_v^t + U^fh_k^{t-1} + b^f)\)

출력 게이트 \(o_v^t = \sigma(W^ox_v^t + U^o {\tilde h_v^{t-1}} + b^o)\)

\(u_v^t = tanh(W^ux_v^t + U^u {\tilde h_v^{t-1}} + b^u)\)

메모리 셀 \(c_v^t = i_v^t \bigodot u_v^t + \sum_{k \in N_v} f_{vk}^t \bigodot c_k^{t-1}\)

은닉 상태 \(h_v^t = o_v^t \bigodot tahn(c_v^t)\)

2. N-ary Tree-LSTM

  • 트리의 각 노드 자식 수가 K보다 작고 자식들에게 1부터 K까지 순서를 매길 때 사용

\(i_v^t = \sigma(W^i x_v^t + \sum_{l=1}^K U_l^i h_{vl}^{t-1} + b^i)\)

\(f_{vk}^t = \sigma(W^f x_v^t + \sum_{l=1}^K U_{kl}^f h_{bl}^{t-1} + b^f)\)

\(o_v^t = \sigma(W^o x_v^t + \sum_{l=1}^K U_t^o h_{vt}^{t-1} + b^o)\)

\(u_v^t = tanh(W^ux_v^t + \sum_{l=1}^K U_l^u h_{vl}^{t-1} + b^u)\)

\(c_v^t = i_v^t \bigodot u_v^t + \sum_{l=1}^K f_{bl}^t \bigodot c_{vl}^{t-1}\)

그래프 LSTM

Sentence-LSTM(S-LSTM)

텍스트를 그래프로 변환하고 그래프 LSTM을 이용해 학습

논문:Sentence-state LSTM for text representation

음.. 이건 약간 자연어 처리 쪽..

그래프 어텐션 네트워크

GAT

Graph Attention Networkx

GaAN

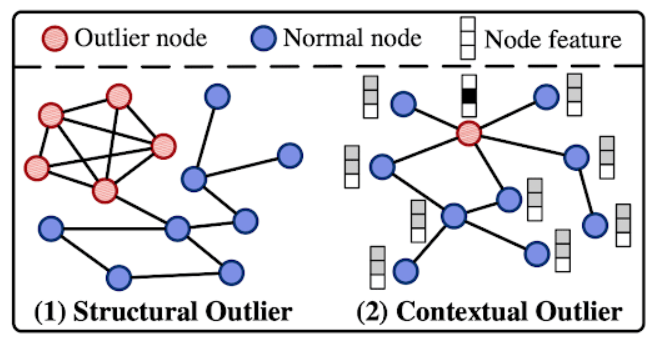
Graph Neural Network-based Graph Outlier Detection: A Brief Introduction

ref: https://www.tigergraph.com/blog/graph-neural-network-based-graph-outlier-detection-a-brief-introduction/

(1)구조적이상치 (2)상황적이상치